6-02-1: 光電効果

さっそく原子物理の3大分野の第1から始めるとしましょう！　→　＜続き＞は6-02-2へ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　6-01-1の冒頭で触れた「19世紀末の当時不可解と思われていた様々な現象」の第１弾が光電効果である。アインシュタインがこの現象を1905年に解明し、後にノーベル賞を受賞した。当時何がどう不可解だったのかは6-04-1まで後回しにし、ここでは後知恵を持つ現代人の明解な目線で、ポイント(I),(II),(III)を順次押さえていくことにする。
　高校物理で扱われる光電効果という現象は図１のようなものである。金属の表面に光を当てると、金属中にある電子が光子のエネルギーを吸収し、金属表面から飛び出してくる現象。6-01-1で述べた通り、1sあたり大まかに10\(^{15}\)個もの光子が降り注ぐが、必ずこの反応は１光子－１電子の対で起こり、この際光子は消滅する。原子物理分野に独特の反応だと理解すればよい。

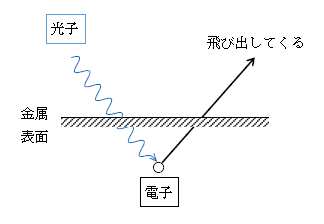
　飛び出してくる電子の中には運動エネルギーが大きいものも小さいものもある。アインシュタインは卓越した洞察で、最も運動エネルギーの大きい電子に注目するとともに、仕事関数\(W\)なる物理量を導入した。
　仕事関数\(W\)=1電子を取り出すために最小限必要な仕事
物質は通常は安定だから、金属からタダで電子が飛び出してくることなどない（仮に電子が飛び出してくるとしたら、何の仕事も加えることなく金属が勝手に壊れていくことを意味する）。仕事関数は金属の種類ごとに決まっていて、亜鉛は\(W\)=3.9eV、セシウムは1.9eVで金属中で\(W\)最小である。
　ここで、最も速く飛び出してくる電子の運動エネルギーを\(K_m \)、入射光の振動数を\(\nu\)とすれば、 光電効果のエネルギー保存則(ポイント(I))は次のように表される。
　 (最速電子の運動エネルギー)=(1光子のエネルギー)\(-\)(仕事関数)
(I)　　　　 \(K_m \; \)　　　　　　 =　　　 \(h\nu\) 　　　　 \(-\)　\(W\)　　
これは　　　たくわえのmax　 =　　　供給　　　　　\(-\) 消費のmin　のように解釈できる式である。
　この式からすぐ分かるのは、光の振動数\(\nu\)を小さくしていくと\(K_m \)=0となること。最も速い電子の運動エネルギーが0ということは、速い電子から遅い電子までひっくるめて、金属表面から電子がぎりぎり飛び出すか飛び出さないかの境目の状況であることを意味する。このときの振動数を限界振動数\(\nu_0\)、波長を限界波長\(\lambda_0\)と呼ぶ。すなわち
(II)　\(K_m =0=h\nu_0-W \) 　　　∴　 \(\displaystyle W=h\nu_0=h\frac{c}{\lambda_0} \)
限界振動数\(\nu_0\)または限界波長\(\lambda_0\)を測定すれば、仕事関数\(W\)が求まる。

　さて、光電効果でよく題材となるグラフの１つ目が図２である（２つ目のグラフは次の単元6-02-2で扱う）。横軸の入射光の振動数\(\nu\)の関数として、縦軸に\(K_m \)を取ったグラフ。ということは\(\nu\)を数学で言う所の横軸\(x\)、\(K_m \)を縦軸\(y\)と見なすという意味だから、
(I)　\(K_m=h\nu -W \)　は
　　[ \(y　=ax+b \) ]　のように見なして、傾き\(h\)、縦軸切片\(-W\)の図２Aのようなグラフとなる。横軸切片は縦軸\(K_m \)=0となる所だから、(II)により限界振動数\(\nu_0\)である。このように、横軸\(\nu\)と縦軸\(K_m \)の測定をするだけで、プランク定数(傾き)\(h\)、仕事関数\(W\)(縦軸切片の絶対値)、限界振動数\(\nu_0\)(横軸切片)が全て実験的に求まる。

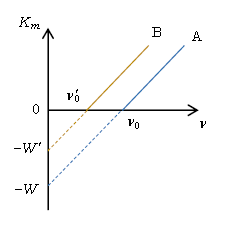
　ここで、別の種類の金属を用いると、仕事関数の値は\(W\)とは異なる\(W’\)のようになるが、グラフの傾きはプランク定数\(h\)でまさに定数だから、図２Bのような、Aと同じ傾きのグラフが得られる。
　なお、縦軸の\(K_m \)を求めるには、次の単元6-02-2で扱う「阻止電圧」を測定すればよい。