5-08-1: 内部エネルギー

熱力学をマスターするには、多原子分子気体の内部エネルギー変化をしっかり押さえることが重要です！　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　まずはモル比熱なる量の定義から。5-02-1の通り、比熱\(c\)とは、ある物質1\(\text{g} \)(または1\(\text{kg} \))あたりの温度を1Kあたり変化させるために必要な熱量。気体を扱うときは\(\text{g} \)よりもモル数の方が便利なので、1\(\text{g} \)あたりではなく1molあたりを考えて、モル比熱\(C\)(大文字の\(C\))を次のように定義する ――
　モル比熱\(C\)=1molあたりの温度を1Kあたり変化させるために必要な熱量 [J/mol\(\cdot \)K]
　\(\displaystyle \)\(n\)[mol]の気体の温度を\(\Delta T\)[K]変化させるために必要な熱量が\(Q\)[J]ならば、
　　\(\displaystyle C=\frac{Q}{n\Delta T} \)　すなわち　\(Q=nC\Delta T \)　　　　　　　　　　　　　　(1)
モル比熱\(C\)も、比熱\(c\)と同様に「ものの温めにくさ(冷めにくさ)の度合い」という意味を持つ。

　では、内部エネルギー\(U\)について5-04-3よりも詳しく説明していこう。以下ではモル数\(n\)一定とする。
　単原子分子気体では5-04-3の通り\(\displaystyle U=\frac{3}{2}nRT\)（\(R\): 気体定数、\(T\): 絶対温度）だから、内部エネルギー変化\(\displaystyle \Delta U=\frac{3}{2}nR\Delta T\)である。
　一方、多原子分子（H\(_2\)、O\(_2\)などの2原子分子、CO\(_2\)などの3原子分子、NH\(_3\)などの4原子分子、…）気体では、結論を先に言えば、\(\displaystyle \frac{3}{2}R\)より大きい定数\(a\)を用いて\(\Delta U=an\Delta T\)となる。　　(＊)
　以下(＊)について説明していく。まず、静止した容器内の気体の内部エネルギーとは次の1．2．の和である。
　　1.　分子各々の運動エネルギーの総和
　　2.　分子間力による位置エネルギーの総和
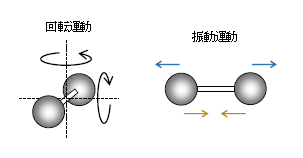
　我々の扱っている理想気体とは、ミクロには分子の衝突時以外は分子間力が無視できる気体（5-04-1）だから、2．は考えなくてよい。つまり、内部エネルギー＝１．である。単原子分子で運動エネルギーと言えば\(\frac{m}{2}v^2\)（並進運動のエネルギーという）のみだが、多原子分子では、それ以外に回転運動のエネルギーや振動運動のエネルギーなども入ってくる（図１）ことに注意しよう。
　5-04-3では、単原子分子気体の\(U\)=分子各々の運動エネルギーの総和
　　\(\displaystyle =N \cdot \overline{\frac{m}{2}v^2} \)\(=\)（途中略）\(\displaystyle =\frac{3}{2}nRT \)　を導いた。ところが、
　多原子分子気体の\(\displaystyle U=N \cdot \overline{\frac{m}{2}v^2}+ \)（回転・振動運動などのエネルギーの総和）　であるから、\(\displaystyle U=\frac{3}{2}nRT+\)〇〇　　のように何らかの〇〇が付け加わる。すると、単原子分子気体の\(\displaystyle \Delta U=\frac{3}{2}nR\Delta T\)に付け加えて、多原子分子気体では(＊)のように\(\displaystyle \Delta U=an\Delta T\)（ただし\(\displaystyle a>\frac{3}{2}R\)）となるであろう。
[ あえて「…だろう」という表現を用いたのは、〇〇を正確に数式で表現するには大学の課程の統計力学や量子力学が必要となり、とても高校物理ではカバーしきれないからである。高校の熱力学としては、(＊)を正しい結論と認めて話を進めていけばよい。]
　ここで\(\displaystyle a=\frac{3}{2}R\)も含めて\(\displaystyle a≧\frac{3}{2}R\)としてやると、\(\Delta U=an\Delta T\)は単原子・多原子両方の場合に成り立つ式となる。　　(☆)

　さて、状態変化には、体積\(V\)一定の定積変化、圧力\(P\)一定の定圧変化、温度\(T\)一定の等温変化、熱量\(Q=0\)の断熱変化、…などいろいろある。が、(☆)から分かることは、（\(n\)が一定なら）多原子・単原子両方について
　\(\Delta U=an\Delta T\)は\(\Delta T\)のみで決まり、途中の状態変化のしかたによらない　(2)
ということである。言い換えると、温度変化\(\Delta T\)が同じなら、定積・定圧・等温・断熱・…全ての変化で内部エネルギー変化\(\Delta U=an\Delta T\)は等しい。
　ところで、定積変化におけるモル比熱を定積モル比熱\(C_V\)という。(1)より
　\(\displaystyle C_V=\frac{定積変化のQ}{n\Delta T}\)　
　熱力学第１法則\(Q=\Delta U+W\)において、定積変化では\(W=0\)（5-06-1）であることを用いると、定積の\(Q=\Delta U\)、つまり
　\(\displaystyle C_V=\frac{\Delta U}{n\Delta T}\)　　　∴　定積の\(\Delta U =nC_V\Delta T \)　　　　　　　　　　　 (3)
　(2)、(3)を組合わせてみる。「　(2)\(\Delta U=an\Delta T\)が状態変化のしかたによらず、一方で定積変化を利用して(3)\(\Delta U =nC_V\Delta T \)と求まったということは、2式を見比べて\(a=C_V\)が言えて、しかもこの\(a=C_V\)は状態変化のしかたによらず成り立つ。　」　　(＃)
　こうして、熱力学分野をマスターするのに欠かせない非常に重要な結論が導ける ――
　　全ての状態変化について、
　　多原子分子・単原子分子気体の内部エネルギー変化\(\Delta U =nC_V\Delta T \)　　 (4)
　この式中の\(C\)に添え字\(V\)が含まれているからといって、(4)が定積変化のみで成り立つと理解するのは全くの誤りである。もう1回(＃)のカギかっこを読み返してほしい。
　なお、単原子分子気体の\(\displaystyle \Delta U =\frac{3}{2}nR\Delta T \)であるから、(4)と比べて単原子分子気体の\(\displaystyle C_V=\frac{3}{2}R \)　が言える。この式から、気体定数\(R\)の単位はモル比熱\(C\)の単位と等しいことも分かる（ポイントすぐ下の段落にある通り [J/mol\(\cdot \)K]である）。