2-19-1: レンズの公式
屈折の法則に関連してもう1つ、「レンズ」をしっかり押さえましょう! → <例題>は2-19-2へ
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント(I) は実像ができる場合(実像の意味はポイント(II)の後で)
ポイント(II)は虚像ができる場合(虚像の意味もポイント(II)の後で)
ポイント(I) <実像ができる場合>
・ 凸レンズ 次の3本の光線のうち2本を使えば、像が作図できる(図1)
光軸平行に進む光は → 後方の焦点を通る (図中の①)
レンズの中心を通る光は → 直進する (②)
前方の焦点を通る光は → 光軸平行に進む (③)
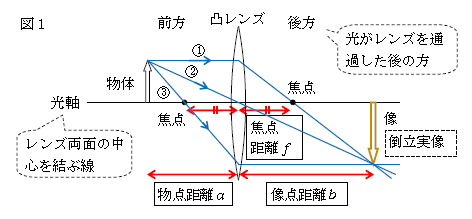
・ レンズの公式 \(\displaystyle \frac{1}{a} +\frac{1}{b} =\frac{1}{f} \)
・ 倍率\(\displaystyle =\frac{像の高さ}{物体の高さ} = \)\(\displaystyle \frac{b}{a} \)
レンズを通過する光は、屈折の法則に従って実は2回屈折する(下の図a)。しかし、簡単のため図1①、②、③のように屈折1回(または0回)として作図してしまう。特に、光軸(レンズ左面の中点と右面の中点どうしを結ぶ線)に平行な光が再び光軸と交わる点を凸レンズの焦点という。また、光がレンズを通過する前の側を前方、通過した後の側を後方という。なぜ①~③のように光は進むのか。レンズに屈折の法則を適用して、さらに2つの条件を課せば、理由は証明できるとだけ言っておこう。当面は①~③を暗記すればよい。
さて、物体は太陽光や室内灯から光を受けてそれを乱反射する(図b)。乱反射された無数の光のうち、特に重要なのは①~③の3本(青線)だが、実はレンズを通過する様々な光全て(太線も含めて)がレンズの後方の1点で交わる。凸レンズはそういう機能を持つ。
ところで人間にはなぜ矢印の形をした物体が見えるのか。人間の「眼は1点から光が広がってくると、そこに点光源があると知覚する」ということに尽きる。矢印のてっぺんから光が無数広がってくるので矢印のてっぺんが知覚され、矢印の真ん中から光が無数広がってくるので矢印の真ん中が知覚され、・・・、結局矢印全体が知覚され、ということなのだ。\(\displaystyle \)
\(\displaystyle \)凸レンズによって光が1点に交わった場所(図bの☆)は、そのまま光線を延長すれば1点から光が広がってくる場所でもある。ゆえに「凸レンズによって光が1点に交わった場所に、人間はあたかも物体があるかのように知覚する」、それを 像 という。なお、図1の「倒立実像」という用語については、次のポイント(II)の後で解説しよう。
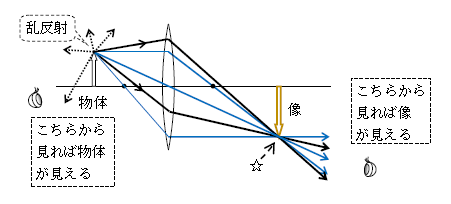
図1 ―― レンズの中心から物体、像、焦点までの距離をそれぞれ\(a,b,f\)と呼び、それらの関係
\(\displaystyle \frac{1}{a} +\frac{1}{b} =\frac{1}{f} \)
をレンズの公式という。その証明は以下の倍率(1)式の説明の後に示す。
倍率とは\(\displaystyle \frac{像の高さ}{物体の高さ}\)のことで、まさに物体に比べて像が何倍に拡大(あるいは倍率が1より小さければ縮小)されるかの比率を表す。図cの斜線を引いた2つの直角三角形の相似より
倍率=\(\displaystyle \frac{高さ}{高さ} =\frac{底辺}{底辺}
=\)\(\displaystyle \frac{b}{a} \) (1)
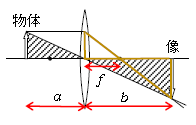
※ レンズの公式の証明を以下に示す。
図cの黄色い2つの直角三角形の相似より
倍率=\(\displaystyle \frac{高さ}{高さ} =\frac{底辺}{底辺} =\)\(\displaystyle \frac{b-f}{f} \) (2)
(1)(2)は等しいものだから \(\displaystyle \frac{b}{a} =\frac{b-f}{f} \)
∴ \(bf=a(b-f) =ab-af\)
両辺\(abf\)で割って \(\displaystyle \frac{1}{a} = \frac{1}{f} -\frac{1}{b} \)
∴ \(\displaystyle \frac{1}{a} +\frac{1}{b} =\frac{1}{f} \)
ポイント(II) <虚像ができる場合>
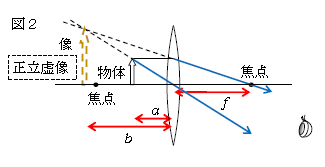
・ 凸レンズ 物体をレンズと焦点の間に置いたとき(図2)
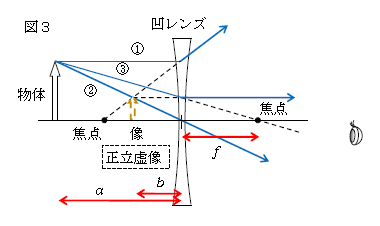
・ 凹レンズ 次の3本の光線のうち2本を使えば、像が作図できる(図3)
光軸平行に進む光は → あたかも前方の焦点から出てくる (①)
中心を通る光は → 直進する (②)
後方の焦点目がけて進む光は → 光軸平行に進む (③)
凹レンズでは(図3とは異なって)物体を焦点とレンズの間に置いても正立虚像ができる
・ レンズの公式では虚像は\(-b\)、さらに凹レンズは\(-f\)を用いる。
つまり図2では \(\displaystyle \frac{1}{a} +\frac{1}{-b} =\frac{1}{f} \)
図3では \(\displaystyle \frac{1}{a} +\frac{1}{-b} =\frac{1}{-f} \)
・ 倍率\(\displaystyle =\frac{像の高さ}{物体の高さ} =\frac{b}{a} \) は図2、図3ともに成立する。
図2の像の見え方を説明しよう。
ポイント(I)に関連して、「眼は1点から光が広がってくるとそこに点光源があると知覚する」と述べた。もう1つの知覚の仕方は、「眼は光が直進してくるものと知覚する」(屈折してくるとは知覚しない)。図2の点線矢印のてっぺんから光が直進してくるとは知覚するが、実線矢印のてっぺんから屈折してくるとは知覚しない。よって点線矢印のような像が見える。
図2の像は正立虚像である。正立とは像が物体と同じ向きに立っているという意味。虚像とは像の場所に実際に光が無数集まっているわけではないという意味(実線は光線の通り道だが、点線には現実の光線は存在しない)。したがって、虚像の場所にスクリーンを置いたとしても何も写らない。
一方、図1の像は倒立実像である。倒立とは像が物体と逆向きに立っているという意味。実像とは像の場所に実際に光が無数集まっているという意味。実像の場所にスクリーンを置くと、確かに像が写る。
以上、図1、図2、図3、全部で3つのパターンの作図は、「自分の手で」実際に練習しておくことが大事。
→ <例題>は2-19-2へ


