2-21-2: ２スリットの干渉 ＜例題＞

２スリットの経路差の計算法が何と言っても大事です！　　　　　　　　　　　　　　　　　　

例題　

　図１のように、光源から出た単色光をスリットSに通し、さらに近接した２本のスリッA、Bに当てたところ、スクリーン上に明暗の縞（干渉縞）が現れ、点Oに最も明るい明線が見られた。スリットA、BはSから等距離におかれている。

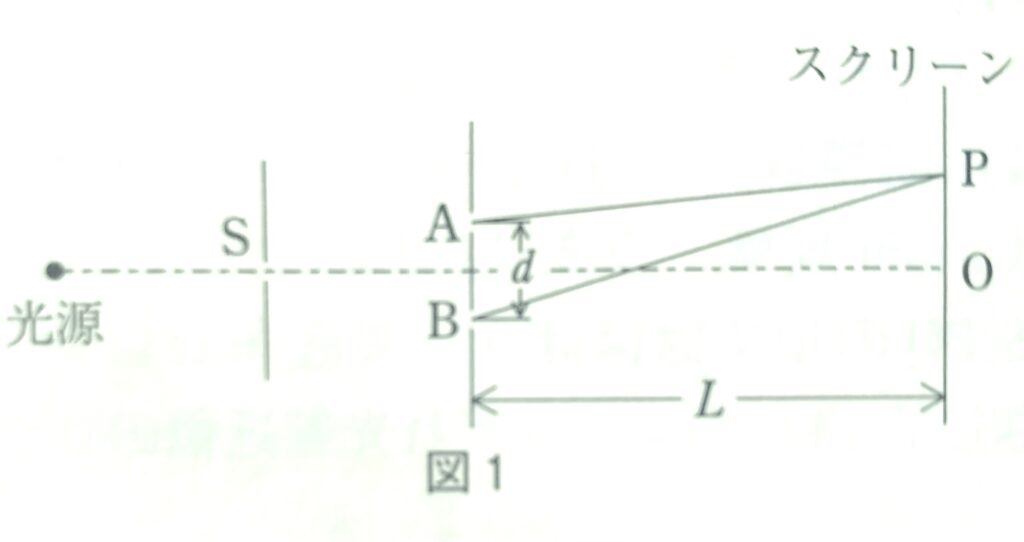
問１　スリットAとBの間隔$d$、またはスリットからスクリーンまでの距離$L$を大きくしたとき、干渉縞の隣り合う明線の間隔はどのように変化するか。正しいものを、次の①～④のうちから一つ選べ。
①　$d$を大きくすると大きくなり、$L$を大きくすると小さくなる。
②　$d$を大きくすると小さくなり、$L$を大きくすると大きくなる。
③　$d$を大きくしても$L$を大きくしても、大きくなる。
④　$d$を大きくしても$L$を大きくしても、小さくなる。

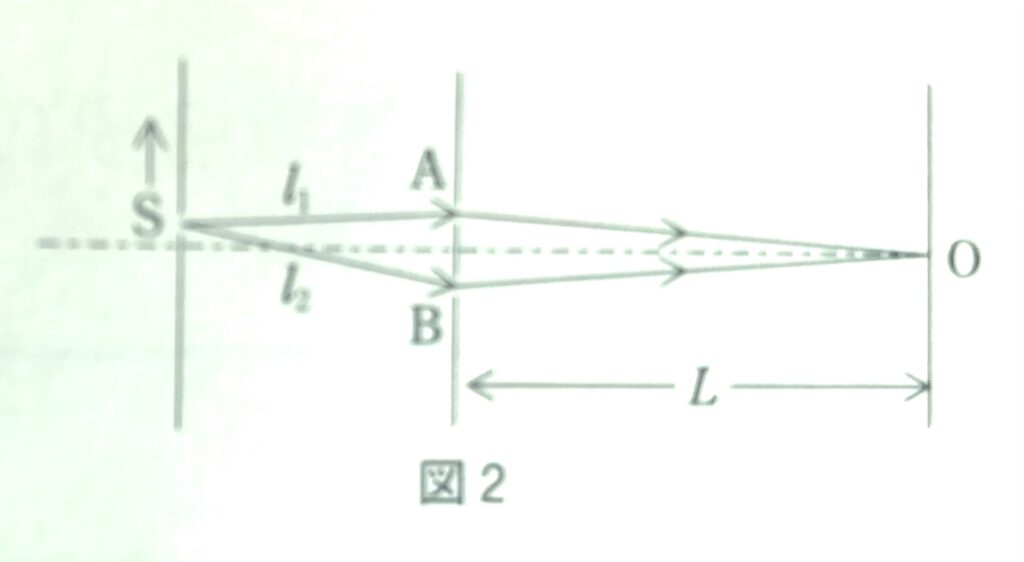
問２　次に、図２のようにスリットSを矢印の向きに動かすと、スクリー上の干渉縞の位置が移動した。点Oの位置が暗線となる条件を満たすものを、次の①～④のうちから一つ選べ。ただし、スリットSからABまでの距離をそれぞれ$l_1,l_2$とする。
①　$l_2-l_1=\lambda$　　②　$\displaystyle l_2-l_1=\frac{5}{4}\lambda$　　③　$\displaystyle l_2-l_1=\frac{3}{2}\lambda$　
④　$\displaystyle l_2-l_1=\frac{7}{4}\lambda$　

解答・解説

　[ 明線間隔を聞かれたのだから、まず強め合いの条件を求めようと考えよう。次に、強め合いの条件には経路差が必要だと考えよう ]
問１　2-21-1でやった通り、経路差$\displaystyle =d\sin\theta ≒d\tan\theta =d\frac{x}{L}$　 (＊)
　強め合いは経路差$\displaystyle d\frac{x}{L} =m\lambda$　（$m=0,\pm 1,\pm 2,\cdots$）　　　
　ゆえに明線の位置は $\displaystyle x_m=m\frac{L\lambda}{d} =0,\,\pm\frac{L\lambda}{d},\, \pm2\frac{L\lambda}{d},\, \cdots$　　　　　　
　これは公差$\displaystyle \frac{L\lambda}{d}$の等差数列だから、となり合う明線の間隔も$\displaystyle \frac{L\lambda}{d}$で、それは$d$を大きくすれば小さくなり、$L$を大きくすれば大きくなる。　　　　答　②
・　以上から分かる通り、明線の位置の公式$\displaystyle x_m=m\frac{L\lambda}{d}$を無理に覚えようとする必要はなく、(＊)の経路差の求め方を理解しておけばよい。

問２　図２より、経路差=(SB+BO)$-$(SA+AO)　　
　BO=AOにより経路差=SB$-$SA=$l_2-l_1$　
　弱め合いはこれが$\displaystyle \left(m+\frac{1}{2} \right) \lambda =\pm\frac{1}{2} \lambda,\, \pm\frac{3}{2} \lambda,\, \pm\frac{5}{2} \lambda,\, \cdots$ に等しくなるときで、選択肢に合うものは③の$\displaystyle \frac{3}{2} \lambda$ 　　　　答　③