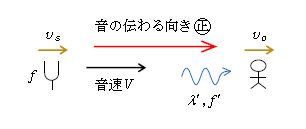
2-13-1: ドップラー効果
重ね合わせの原理からはいったん離れて、ドップラー効果なる重要な現象を扱います。 → <例題>は2-13-2へ
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
ドップラー効果
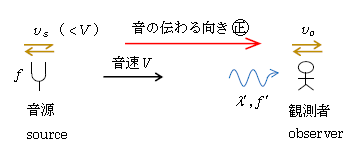
・ 音速\(V\)は、音源が静止しているか運動しているかによって変わらない
・ 音源が動くと波長が変化する。観測者に届く波長 \(\displaystyle \lambda '=\frac{V-v_s}{f} \)
・ 観測者が動くと音速が相対速度\(V’=V-v_o\)になる
・ 観測者に届く振動数 \(\displaystyle f’ =\frac{V’}{\lambda '} =\frac{V-v_o}{V-v_s} f \)
音の高低は振動数で決まる。音が高いとは振動数が大きいということ。ならば、「パトカーのサイレンはパトカーが近づくときには高く聞こえ、遠ざかるときには低く聞こえる」は、「音源が近づいていると振動数は大きくなり、遠ざかっていると小さくなる」と言いかえられる。このように、音源(または観測者)の間に相対的な運動があるとき振動数が変化する現象をドップラー効果という。なお、観測者が音源に近づいているとやはり振動数は大きくなり、遠ざかっていると小さくなる。
ドップラー効果は2部構成。(I) 音源が運くことによるドップラー (II) 観測者が運くことによるドップラー 以下この順序で説明していく。
(I) 音源が動くとき
理解しておくべきことは1⃣ 2⃣ の2つ。
1⃣ 音速は、音源が静止しているか運動しているかによって変わらない。
10m/sで動くおんさから340m/sの音が発せられたとしても、音速は10+340=350m/s(合成速度)にはならず340m/sである。なぜか。一言で言えば「それが波動の法則性」ということ、それでよい。(が、参考までに補足すると ―― 2-01-1でやった通り、波動では媒質粒子は中心のまわりに振動するのみで、遠くへ遠くへ移動していかない。遠くへ伝わるのは振動、つまり、一つの粒子の振動が少しずつ遅れたタイミングで隣りの、そのまた隣りの粒子の振動を引き起こしていく。その振動の伝わる速さが波の速さだから、それはひとえに振動を伝える媒質の性質だけによって決まる。波源を動かしても、振動を伝える媒質の性質を変えない限り、振動の伝わる速さ(波の速さ)は変えられないのだ。)
2⃣ 波長は変化する
これを理解するために、まず音源(おんさ)が静止しているときの波面の様子を押さえよう(図1)。音は、発せられて後1s間に音速\(V\)×1s進み、波面は半径\(V\) の球面となる。1s間におんさは振動数\(f\)回振動して\(f\)個の波を出すから、1s後の波面の数は\(f\) 個(図1では\(f\) =3Hzとした)。すると
\(\displaystyle \lambda =\)波1個の長さ\(\displaystyle =\frac{V}{波の数} =\frac{V}{f} \)
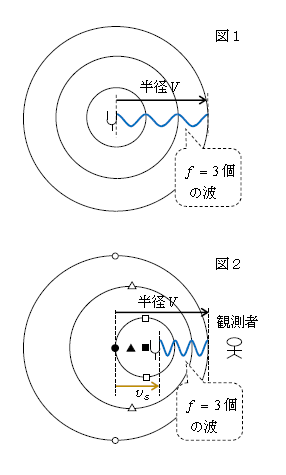
一方、音源が速度\(v_s\) で観測者に近づいていくと図2のようになる。0sで●から発信される音は、1s間に\(V\) 進んで半径\(V\) の球面(○印)となる(1⃣ 音速は音源が動いても\(V\) のまま)。\(\frac{1}{3}\)sで▲から出る音は、1s後までの\(\frac{2}{3}\)s間に\(\frac{2}{3} V \)進んで半径\(\frac{2}{3} V \)(△印)、\(\frac{2}{3}\)sで■から出る音は、1s後までの\(\frac{1}{3}\)s間に\(\frac{1}{3} V \)進んで□印。ゆえに1s後の波面は図2となり、\(V-v_s\)中に\(f=3\)個の波が入っていることが見て取れる。よって観測者へ届く波長
\(\displaystyle \lambda ' =\)波1個の長さ\(\displaystyle =\frac{V-v_s}{波の数} =\)\(\displaystyle \frac{V-v_s}{f} \) (1)
\(\displaystyle \)図1と2を見比べると、音源静止の図1では、\(V\) の中に\(f\)個の波が入るから\(\displaystyle \lambda =\frac{V}{f}\)。観測者に近づく図2では、\(V\)より短い\(V-v_s\)中に\(f\)個の波が入るから、\(\lambda '\)は\(\displaystyle \frac{V}{f} \)より短く\(\displaystyle \lambda '=\frac{V-v_s}{f}\) 。音源が近づくとき波長は縮むと分かる。
ドップラー効果は、「自分の手で」図2の作図をしながら理解し、かつ波長公式(1)を覚えることが大事。図2も波長公式もよく出題のテーマになる。
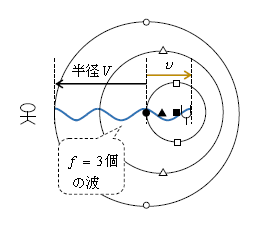
念のため、音源が観測者から速さ\(v\)で遠ざかっている場合を考えよう。これは図2で観測者が左側に位置している場合と考えればよい(図3)。\(V+v\)中に\(f\)個の波が入っているから、観測者へ届く波長
\(\displaystyle \lambda '=\)波1個の長さ\(\displaystyle =\frac{V+v}{波の数} =\frac{V+v}{f} \) (*)
つまり\(\displaystyle \lambda '>\frac{V}{f}=\lambda \)だから、音源が遠ざかるとき波長は伸びると分かる。
さて、ドップラー効果では音の伝わる向きを速度の正の向きに取ると覚えるとよい(図3では左向き)。図3中の速さ\(v\)は右向きだから、音源の速度としては\(v_s=-v\)である。これを(*)に代入すれば
\(\displaystyle \lambda '=\frac{V-v_s}{f}\) で、やはり(1)が成立している。
(II) 観測者が動くとき
理解しておくべきことは、音が動く観測者に対して相対速度(相対音速)\(V’\)でやってくるということ。1⃣で述べたように音源が運いても音速は変わらないが、観測者が動くと相対的な音速になるという意味だ。図4のように音の伝わる向きを正として観測者の速度\(v_o \)とする。 動く観測者に対する相対速度は「に対するを引く」と得られる(1-30-1)から、
相対音速\(V’=V-v_o\) (2)
(1)(2)を組合わせると、ドップラー効果の振動数公式が得られる
縮んだ(伸びた)波長\(\lambda ' \) (1) が、相対音速\(V’\) (2) でやってくるのだから、観測者に届く振動数\(f’\)は
\(\displaystyle f’=\frac{V’}{\lambda '}=\)\(\displaystyle \frac{V-v_o}{\frac{V-v_s}{f}}=\)\(\displaystyle \frac{V-v_o}{V-v_s} f \) (3)
(1)(2)を組合わせた(3)の式変形を何回か練習すれば、振動数公式は容易に頭に入るだろう。
ここで、例えば音源が近づき観測者が静止している場合を考えると、図4より\(v_s>0,v_o=0\)だから(3)は\(\displaystyle f’=\frac{V}{V-v_s} f \) となる 。\(\displaystyle \frac{V}{V-v_s}\)は(分母より分子の方が大きく)1より大きいから\(f’>f\) 、これはポイントすぐ下の段落中に述べたことと合う。
また、観測者が近づき音源が静止している場合、図4より\(v_s=0,v_o<0\)だから(3)は\(\displaystyle f’=\frac{V-v_o}{V} f \) 。\(v_o<0\)だから\(V-v_o>V\) すなわち\(\displaystyle \frac{V-v_o}{V}\)は(分母より分子の方が大きく)1より大きいから\(f’>f\) 、これもポイントすぐ下で述べたことと合う。