2-09-3: 水面波の干渉 ＜例題＞＜動画あり＞
水面を伝わる波の干渉の問題を練習しておきましょう！
※ ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
例題
図のように、水面上の距離\(l\)だけ離れた２点A、Bに波源があり、この二つの波源から同じ振幅、同じ振動数の水面波が出ている。距離\(l\)はこの波の波長の３倍である。
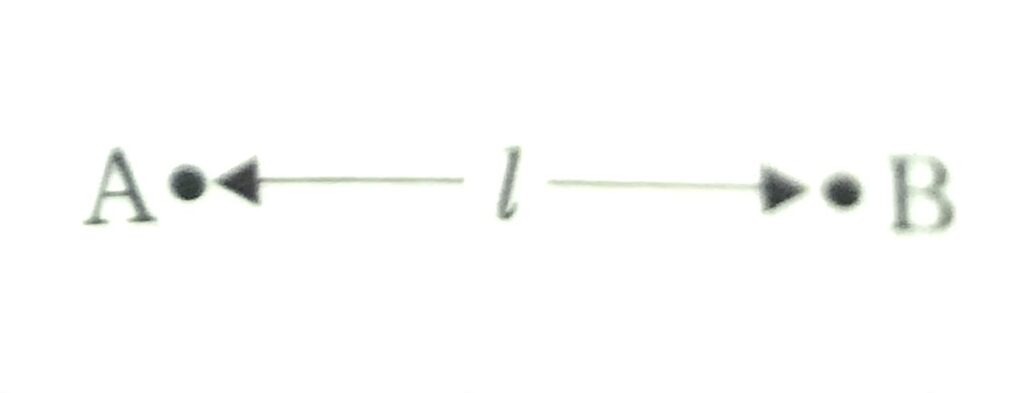
問１ Aの波源とBの波源の振動が同位相の場合、水面上で、波が強め合って振幅が大きくなる点をつないだ曲線の形はどれか。次の①～⑤のうちから正しいものを一つ選べ。
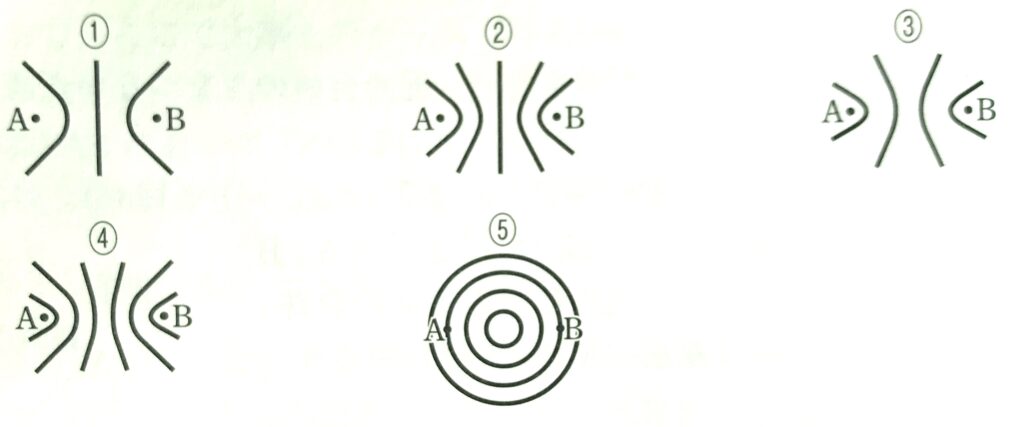
問２ 問１で、水の深さを変えたところ波の速さが大きくなった。直線AB上で波が強め合う位置はどのように変化するか。次の①～④のうちから正しいものを一つ選べ。
① 波が強め合う位置の間隔は狭くなり、それらの位置は直線ABの中心に寄ってくる。
② AB間の距離が波長の3倍からずれるので、AB上には波が強め合う位置は生じない。
③ 波が強め合う位置の間隔は広くなり、それらの位置は直線ABの中心から離れてくる。
④ 波の速さが変わっても、波が強め合う位置は変化しない。
問３ Aの波源とBの波源の振動が逆位相の場合、ABの垂直２等分線Mの上で、水面の振動のようすはどうなるか。次の①～③のうちから正しいものを一つ選べ。
① いたる所で波は強め合う。
② いたる所で波は弱め合う。
③ 波が強め合う位置と弱め合う位置が交互に生じる。
解答・解説
問１ 図１で
強め合いの条件は経路差PA\(-\)PB\(=m\lambda =0,\pm \lambda ,\pm 2\lambda ,\cdots \)
弱め合いの条件は PA\(-\)PB\(=(m+\frac{1}{2}) \lambda =\pm \frac{1}{2} \lambda , \pm \frac{3}{2} \lambda ,\cdots \)
強め合いの点をつないだ線を腹線、弱め合いの点をつないだ線を節線という（図２）。四角の囲みに書いてある通り、実線が山の波面、点線が谷の波面、丸印(実線点線両方)が強め合いの位置で、バツ印が弱め合いの位置。ゆえに腹線は丸印をつないだ赤線、節線はバツ印をつないだ黄色の線となっている。
例えば経路差PA\(-\)PB\(=-2\lambda \)の式は、「２定点A、Bからの距離の差が一定値 \(-2\lambda \)となる点Pの軌跡」と読めるから、軌跡は双曲線である(図２中の☆を付けた赤線)。山と谷の間隔が\(\frac{1}{2} \)波長であることに注意して、確かにPA\(-\)PB\(=-2\lambda \)となっていることを確認しよう。
他にもPA\(-\)PB\(=\lambda \)の腹線(赤線)上に点Pを持ってくると、本当にPA\(-\)PB\(=\lambda \)になっているなど、チェックしておくとよい。
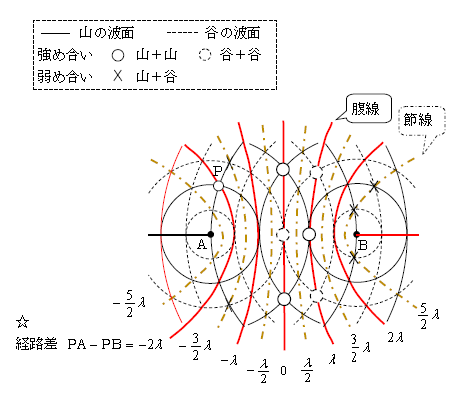
さて、ここで大事なのが三角不等式――三角形の２辺の和は他の一辺より大きく、２辺の差は他の一辺より小さい――である。すると図２の△PABにおいて\(|\)PA\(-\)PB\(|<\)AB。問題文にある通りAB\(=l=3\lambda \)だから、\(|\)PA\(-\)PB\(|<3\lambda \)。ゆえに双曲線タイプとして現れるのは、図２で\(\frac{5}{2} \lambda \)まで。\(4\lambda,\frac{11}{2}\lambda \)などは現れない。
（参考までに、図２でA、Bの左右に伸びる直線タイプは、\(|\)PA\(-\)PB\(|\)がぴったり\(3\lambda \)のものである。つまり、直線タイプの上に点Pがあると、\(|\)PA\(-\)PB\(|=\)AB\(=3\lambda \)となっている。）
まとめると、同位相の波源では次の３点が重要だ。
(1) ABの垂直二等分線は経路差0の腹線である。
(2) その両側に節線、腹線、･･･と交互に双曲線が並ぶ。
(3) 節線、腹線の本数は三角不等式で分かる。 答 ②
問２ 波の速さ\(V=\lambda f \)は大きくなるが、振動数\(f\)は変えないのだから、波長\(\lambda \)が大きくなる。つまり、AB間で節線や腹線の間隔は広くなる。しかも上の(1)にまとめた通り、ABの中点が腹の位置であることに変わりはない。よって 答 ③
問３ 2-09-1にある通り、A、Bが逆位相の波源の場合は、同位相のときと強め合い・弱め合いの条件が逆転する。つまり、同位相のときの腹線・節線が、逆位相ではそれぞれ節線・腹線になる。よって、図２ではABの垂直２等分線は経路差 の腹線だが、これが逆位相では節線になる。 答 ②
なお、michisanpo – YouTubeにある関連動画も是非参考にしてみて下さい。よければチャンネル登録お願いします。
https://www.youtube.com/watch?v=IcpD5xlWiJQ