2-09-1: 干渉

重ね合わせの原理で生じる現象の第３弾 ―― ２つの波の強め合い・弱め合い「干渉」　→　＜例題＞は2-09-2、2-09-3へ　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の $\equiv$ 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

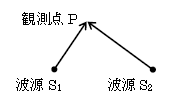
　重ね合わせの原理に基づいて起こる現象として、今度は干渉を考えよう。振幅$A$の２つの波が重なって振幅$2A$になるのを強め合い、振幅0になるのを弱め合いといい、強め合い・弱め合いの生じる現象を干渉という。
　強め合い（図１）は、例えば１つの波の山（変位$A$）と別の波の山（変位$A$）が重なって合成変位$A+A=2A$になったり、谷（変位$-A$）と谷（変位$-A$）が重なって合成変位$(-A)+(-A)=-2A$になる状況である。

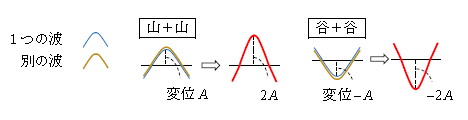
　弱め合い（図２）は、例えば山と谷が重なって合成変位$A+(-A)=0$になる状況。

　さて、水面の１点Sを叩くとSから水面波が四方八方に広がる。波の伝わる大本の点Sを波源という。水面の様子を上から捉えたものが図３。

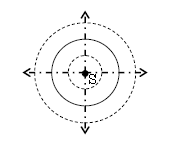
　山の部分は水面（紙面）に垂直に出っ張って実線の円のように、谷の部分は水面（紙面）に垂直にくぼんで点線の円のようになる。それぞれ山の波面、谷の波面という。波面と波の進行方向(１点鎖線)は垂直で、山と山(谷と谷)の波面の間隔は１波長である。
　今度は２点S₁とS₂を同じタイミングで叩く。S₁とS₂を同位相の波源（同じタイミングで振動する波源）という。波を合成する前の様子は、S₁ が山の瞬間にS₂も同じタイミングの山で図４のようになる。
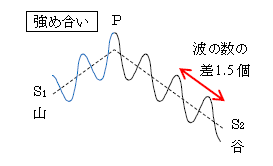
　$\displaystyle$いま、1波長分を波1個と数えることにしよう。また、S₁ 、S₂からの波をそれぞれ波１、波２と呼ぼう。ある観測点Pで波１の山と波２の山が重なって強め合うのは、図５から分かる通り、波１の中に含まれる波の数（2個）と波２の中の波の数（4個）の差がぴったり整数（2個）の場合である。

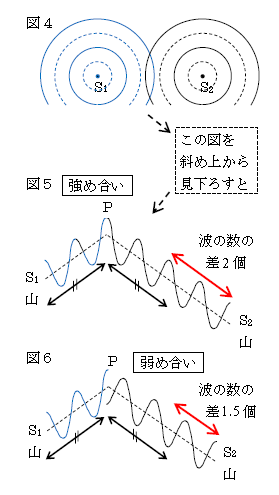
　一方、点Pで波１の山と波２の谷が重なって弱め合うのは（図６）、波１の中に含まれる波の数（2個）と波２の中の波の数（3.5個）の差（1.5個）が整数プラス$\frac{1}{2}$の場合である。
　つまり強め合い・弱め合いは波の数の差が整数か整数＋$\frac{1}{2}$かで決まる。
　ところが波の数の差の付いた図３図４の ←→ の部分は、波源S₁、S₂から観測点Pまでの距離の差S_２P$-$S_１Pに相当する部分で、これを経路差という。波1個分の長さは1波長だから、波の数の差が整数とは、経路差が波長の整数倍ということに他ならない。
　よって同位相の波源では、強め合うのは波の数の差が整数のとき、すなわち経路差が波長の整数倍のときである。弱め合うのは波の数の差が整数＋$\frac{1}{2}$のとき、すなわち経路差が波長の整数＋$\frac{1}{2}$倍のときである。

　S₁ とS₂を逆のタイミングで叩く場合もよく出題される。これを逆位相の波源（逆のタイミングで振動する波源）という。S₁が山谷山･･･と振動するならS₂は谷山谷･･･と振動。S₁ が山の瞬間はS₂は谷である。
　もう、図７から明らかだろう。強め合い・弱め合いの条件は逆位相の波源では同位相のときと逆転し、強め合うのは経路差が波長の整数＋$\frac{1}{2}$倍のとき、弱め合うのは経路差が波長の整数倍のときとなる。