2-09-2: 干渉 <例題>
波の強め合い・弱め合いに関する出題には、干渉条件を用いましょう! → <例題2>は2-09-3へ
例題1
図のように3.0m離れた2点Bに置いたスピーカーから、同じ振動数で、同じ位相、同じ振幅の音を出す。いろいろな場所でスピーカーからの音を聞くと、音が大きく聞こえたり小さく聞こえたりする場所があった。
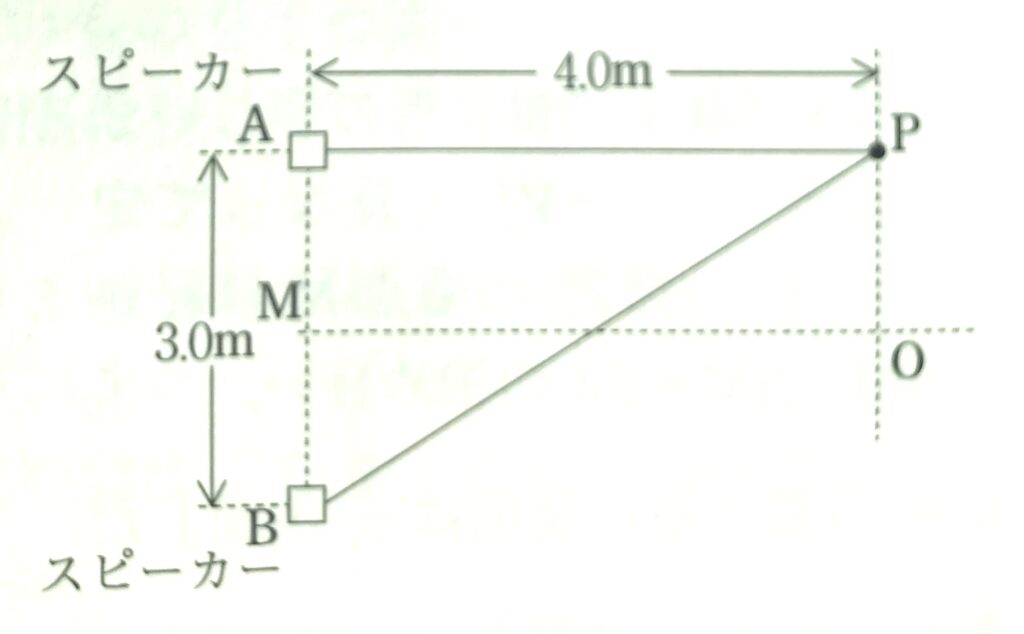
問1 直線ABから4.0m離れ、ABに平行な直線上を観測者が移動していく。2点A、Bから等距離の点Oで聞こえる音が大きくなり、次にOから1.5m移動した点Pで再び聞こえる音が大きくなった。波長は何mか。次の①~⑥のうちから正しいものを一つ選べ。
① 0.5 ② 1.0 ③ 1.5 ④ 2.0 ⑤ 2.5 ⑥ 3.0
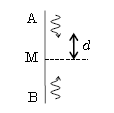
問2 線分AB上で音が大きく聞こえる点の、ABの中点Mからの距離を\(d\)とする。\(d\)は音の波長\(\lambda \)とどのような関係にあるか。次の①~⑥のうちから正しいものを一つ選べ。ただし、\(n\)は0または正の整数である。
① \(\displaystyle \frac{1}{4} \left( n+\frac{1}{2} \right) \lambda \) ② \(\displaystyle \frac{1}{4} n\lambda \) ③ \(\displaystyle \frac{1}{2} \left( n+\frac{1}{2} \right) \lambda \)
④ \(\displaystyle \frac{1}{2} n\lambda \) ⑤ \(\displaystyle \left( n+\frac{1}{2} \right) \lambda \) ⑥ \(n\lambda \)
解答・解説
問1 図1から分かる通り、点Oは経路差BO\(-\)A=0\(\lambda \)の強め合い。
「点Pで再び聞こえる音が大きくなった」ということは、点Pはすぐ隣りの強め合いだから、経路差BP\(-\)AP=1\(\lambda \)。
(2\(\lambda \)や\(-\)3\(\lambda \) のようにはならない)
よって\(\lambda \) =BP\(-\)AP=5.0-4.0=1.0m 答 ②
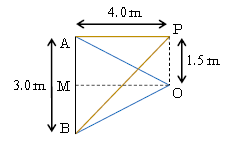
問2 線分AB上では「形の等しい2つの波が\(+V,-V\)」で重なって定常波が立つ(図2)。中点Mは経路差BM\(-\)AM=0\(\lambda \)の強め合い、つまり腹。
[ 2つの波源を結ぶ線分AB上では、干渉を定常波として扱える ]
「腹と腹の間隔は\(\frac{1}{2}\)波長」だから、腹(強め合い)の位置のMからの距離
\(\displaystyle d=0, \frac{1}{2}\lambda, \frac{3}{2}\lambda, \cdots =n\frac{1}{2}\lambda \) 答 ④