2-05-1: 重ね合わせの原理

様々な波動現象を引き起こす、重要な原理をしっかり理解しましょう！　　　　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

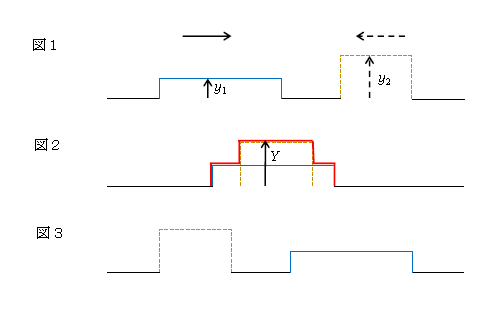
　図１のように、変位(高さ)\(y_1\)の波が右に、変位\(y_2\)の波が左に進んでくると、何が起こるだろうか（現実には、このような角ばった波は存在しないが、簡単のためそれを扱う）。
　２つの波は「ぶつかって」はね返ったりはしない。ただ単に「重なり合い」（図２）、その後、お互い何事もなかったようにすり抜ける（図３）。しかも、重なり合っている間は次の重ね合わせの原理が成り立つ：
　　２つの波が重なり合った所での変位\(Y\)は、２つの波がそれぞれ単独にやってきたとしたときの変位\(y_1\)および\(y_2\)の和に等しい。　　　\(Y=y_1＋y_2\) 
　要は２つの波が重なると、それらの高さが足し算されるということ。変位\(Y\)から成る波を合成波という（図２の赤線）。 

　なぜ２つの波が「ぶつかって」はね返るようなことは起きないのか。一言で言ってしまえば「それが波動の法則性」となるのだが、少し補足しておくと ―― 2-01-1でやった通り、波動では波形は\(x\)方向へ平行移動しても、媒質粒子は\(x\)方向へ移動しない。ただ\(y\)方向に変位するのみである。粒子が\(x\)方向へ移動してきてぶつかることなど、決して起こらない。
　なお、縦波では粒子の変位は\(x\)方向だが、縦波の横波的表示の考え方に基づいて変位を\(y\)方向に取り直せば、このページの結論は縦波でも全て成り立つ。（詳しい話は大学に任せて）「それが波動の法則性」と割り切ろう。