10-04-2: 力学的エネルギー保存則の証明（続き）

このトピックでは2質点の力学的エネルギー保存則特有の重要事項を扱います。　→　10-04-1からの続きです　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　質点１、質点２のそれぞれの位置を\(\vec{r_{1}} \, 、\vec{r_{2}} \)とする。それぞれの位置ごとに位置エネルギー\(U(\vec{r_{1}}) \) 、\(U(\vec{r_{2}}) \) が定まるような場合は（たとえば重力による位置エネルギー\(mgh_1\) 、\(mgh_2\)）、特に前の単元10-04-1に付け足すことはない。しかし、2質点の両方の位置を決めないと位置エネルギーが定まらない場合がある。たとえば弾性力による位置エネルギー\(\frac{k}{2}\)(のび・ちぢみ)\(^2\) 。明らかに(のび・ちぢみ)は片方の質点の位置だけでは定まらず、両方の位置が決まって初めて定まる量である。
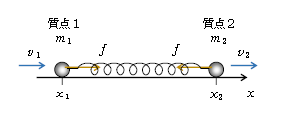
　図１を用いてこのような場合を考察する。質点１、２が軽いばねの両端につながれて1次元運動しており、それぞれの位置を\(x_1 \, 、x_2\)、速度を\(v_1 \, 、v_2\)とする。ばねの自然長を\(l\)とし、ばねが伸びている瞬間の弾性力\(f\)を図示してある。弾性力の向きは自然長に戻ろうとする向き(1-14-1)だから、伸びたばねが両端を引張る向き。また、のび\(=\)(ばねの長さ\(x_2-x_1\))\(-\)自然長\(l\) だから、\(f=k\)×のび\(=k(x_2-x_1-l)\) 。

　加速度\(\displaystyle a_1=\frac{dv_1}{dt} \) 、\(\displaystyle a_2=\frac{dv_2}{dt} \)より運動方程式は
　質点１: \(\displaystyle m_1\frac{dv_1}{dt}=+f=+k(x_2-x_1-l) \)　　　　　　　　　　　　 ①
　質点２: \(\displaystyle m_2\frac{dv_2}{dt}=-f=-k(x_2-x_1-l) \)　　　　　　　　　　　　 ②
　なお、伸びている瞬間について立式したが、縮んでいる瞬間なら ―― ちぢみ\(=\)自然長\(l\)\(-\)(ばねの長さ\(x_2-x_1\))で、弾性力の大きさ\(f’=k\)×ちぢみ\(=k(l-(x_2-x_1))\) 。向きは縮んだばねが自然長に戻りたがって両端を押す向き、すなわち\(f’\)と図１の\(f\)は逆向き。すると質点１の運動方程式は
　\(\displaystyle m_1\frac{dv_1}{dt}=-f’=-k(l-(x_2-x_1))=+k(x_2-x_1-l) \) となって①と同じになる。結局、伸びている瞬間について立式しても縮んでいる瞬間でも、運動方程式は変わらない。質点２も同様である。
　さて、ここで①×\(v_1\)+②×\(v_2\)としてみる。　[ なぜか。こうするとゆくゆくは上手く行くからで、なぜ①×\(v_1+\cdots\)？と手を止めたりせず、話に付いてくることが大切。とは言え、ここからの式変形は少し長い。難しすぎると感じたなら、途中は飛ばして、とりあえず最後のポイントだけ押さえておくのも一法だろう。 ]
　\(\displaystyle m_1v_1\frac{dv_1}{dt}+m_2v_2\frac{dv_2}{dt}=k(x_2-x_1-l)(v_1 -v_2) \)　　　　　　 　 ③
　ところで\(\frac{m_1}{2}{v_1}^2\)を\(t\)で微分すると　[ こうするとゆくゆくは上手く行くから ]
　　\(\displaystyle \frac{d \left( \frac{m_1}{2} {v_1}^2 \right) }{dt}=\frac{d \left( \frac{m_1}{2} {v_1}^2 \right) }{dv_1}\frac{dv_1}{dt}\)　[ つまり合成関数の微分を用いている ]
　　　\(\displaystyle =m_1v_1\frac{dv_1}{dt}=\)③の左辺第1項。　同様に
　　\(\displaystyle \frac{d \left( \frac{m_2}{2} {v_2}^2 \right) }{dt}=\frac{d \left( \frac{m_2}{2} {v_2}^2 \right) }{dv_2}\frac{dv_2}{dt}=\)③の左辺第2項。　ゆえに
　③の左辺\(\displaystyle =\frac{d \left( \frac{m_1}{2} {v_1}^2 \right) }{dt}+\frac{d \left( \frac{m_1}{2} {v_1}^2 \right) }{dt}= \frac{d}{dt} \left(\frac{m_1}{2}{v_1}^2 +\frac{m_2}{2} {v_2}^2 \right) \; \)　 ④
　次に\(\frac{k}{2}(x_2-x_1-l)^2\)を\(t\)で微分してみる。
　　\(\displaystyle \frac{d \left( \frac{k}{2}(x_2-x_1-l)^2 \right) }{dt} \)　[ \(r=x_2-x_1\)とおく ]
　　　\(\displaystyle =\frac{d \left( \frac{k}{2}(r-l) \right)^2}{dr}\frac{dr}{dt}=k(r-l)\frac{dr}{dt} \)　　　　　　　　　　　　　　 ⑤
　　いま \(\displaystyle \frac{dr}{dt}=\frac{d(x_2-x_1)}{dt}=\frac{dx_2}{dt}-\frac{dx_1}{dt}=v_2-v_1 \) だから、⑤の続きは　
　　　\(\displaystyle =k(r-l)(v_2-v_1)=k(x_2-x_1-l)(v_2 -v_1)= \)③の右辺×(\(-1\))　
　すなわち、③の右辺\(=\)⑤の最左辺×(\(-1\))\(\displaystyle =-\frac{d \left( \frac{k}{2}(x_2-x_1-l)^2 \right) }{dt} \;\, \)　　⑥
　④、⑥をそれぞれ③の左辺、右辺に代入　\(\displaystyle \frac{d}{dt} \left(\frac{m_1}{2}{v_1}^2 +\frac{m_2}{2} {v_2}^2 \right)\)
　　　　　　　　　　　　　　　　　　\(\displaystyle =-\frac{d}{dt} \left( \frac{k}{2}(x_2-x_1-l)^2 \right) \)
　　∴　\(\displaystyle \frac{d}{dt} \left(\frac{m_1}{2}{v_1}^2 +\frac{m_2}{2} {v_2}^2+ \frac{k}{2}(x_2-x_1-l)^2 \right) =0 \)
　さて、微分して0になるものは定数だから、上の式の\(\displaystyle \frac{d}{dt} \left( \cdots \right) \) の \(\cdots \) は定数
　よって　\(\displaystyle \frac{m_1}{2}{v_1}^2 +\frac{m_2}{2} {v_2}^2+\) \(\displaystyle \frac{k}{2}(x_2-x_1-l)^2 \)\(=\)一定　　　(☆)
　以上、式変形が長くなったが、(☆)は力学的エネルギー保存則を表している。第１項、第２項は２質点の運動エネルギーを表す。第3項は弾性エネルギー。
　ところで、学生の中にはこう考えてしまう人がいるが、以下は(☆)より誤りである。「弾性エネルギーは質点１，２がそれぞれ持っているのだから、\(\displaystyle \frac{k}{2}(x_2-x_1-l)^2 \) の2倍分ある。」
　正しい結論をポイントとしてまとめておく。しっかり押さえておこう。