10-02-2: 力には向きがある、仕事には向きがない #その２

いよいよ話が佳境に入ってきました！　→　＜#その1＞は10-02-1、＜#その3＞は10-02-3へ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

向きがあるという意味

　ではベクトルには向きがあり、スカラーには向きがない、ということの意味を考えていこう。
　いま図３のように$x$-$y$平面上にベクトル$\vec{c} =(c_x,\, c_y)$を取り、図４のように$x$-$y$軸と角$\theta$をなす$x’$-$y’$軸でベクトル$\vec{c} =({c_x}’,\, {c_y}’)$と成分表示したならば、これらの成分$c_x,c_y,{c_x}’,{c_y}’$の間にはどんな関係が成り立つだろうか。これは「回転変換」（あるいは直交変換）と呼ばれている数学の内容であるが、以下の議論に必要となるので説明していく。少しだけお付き合い願いたい。

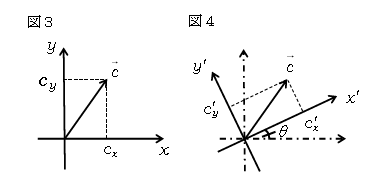
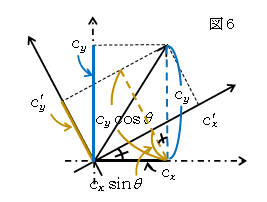
　図５中の赤が${c_x}’$、図６中の黄色が${c_y}’$であることに注意すると、
$$\begin{equation} \tag{☆} \begin{cases} {c_x}’=c_x\cos\theta +c_y\sin\theta \\ {c_y}’=-c_x\sin\theta +c_y\cos\theta \end{cases} \end{equation}$$ 　この規則(☆)は、ベクトルの成分が座標軸の回転に対して持つ重要な性質である。

　例えば10-02-1の小球の例では、重力$\vec{F}=m\vec{g}$について$(F_x,\, F_y) =(0,\, -mg)$であったから、(☆)に代入すると
$$\begin{equation} \begin{cases} {F_x}’=F_x\cos\theta +F_y\sin\theta =-mg\sin\theta \\ {F_y}’=-F_x\sin\theta +F_y\cos\theta =-mg\cos\theta \end{cases} \end{equation}$$ になるはずであるが、実際そうだった（10-02-1）。
　さて、ここからが重要である。物理では、一歩進めて、規則(☆)こそベクトルに「向きがある」ことの具体的な正確な数式的表現であると考える。つまり、
　ある物理量が回転変換に際して規則(☆)に従って変換されたならば、その物理量はベクトルである、その物理量には向きがある
と理解する。我々が直観的に向きを持つと把握するところの矢印で表される物理量（速度など）は、明らかに(☆)に従うから、この理解は受け入れやすい。逆に(☆)を満たさない物理量は、たとえ正負の符号を持つものであってもベクトル量と見なすことはできない。実は「仕事」は、そういう観点からベクトルではなくスカラーなのである。以下このことを見ていこう。

向きがないという意味

　誰もが知っているように、ベクトル$\vec{c}$の大きさ$|\vec{c}|$はスカラーである。スカラーは回転変換によってどのように変換されるのだろうか。
　いま$x$-$y$平面での$\vec{c}$の大きさを$l$と書けば、$l=\sqrt{{c_x}^2 +{c_y}^2 }$。他方$x’$-$y’$平面での$\vec{c}$の大きさ$l’=\sqrt{{c_x}’^2 +{c_y}’^2 }$。ところが(☆)より
　$l’^2=(c_x\cos\theta +c_y\sin\theta)^2 +(-c_x\sin\theta +c_y\cos\theta)^2$
　　[ ${c_x}^2 ,c_xc_y ,{c_y}^2$の項について整理して ]
　　$={c_x}^2 (\cos^2\theta+\sin^2\theta) +2c_x c_y (\cos\theta \sin\theta-\sin\theta \cos\theta)$
　　$+{c_y}^2(\sin^2\theta+\cos^2\theta)　=c_x^2 +c_y^2=l^2$
　∴　$l’=l$
　従ってベクトルの大きさは回転変換に際して不変である。座標軸をどう回そうとも、ベクトルの大きさが変わるはずもないから、容易に納得の行くことだろう。そこで、
　ある物理量が回転変換に際して不変ならば、その物理量はスカラーである、その物理量には向きがない
と理解できる。例えば温度には+15℃もあれば$-$3℃もあり、正負の符号がある。しかし座標軸の方向をどう取っても温度は変わらない。よって温度はスカラーであり、向きがない。結局、回転変換に対する変換性こそが、向きのあるなしの判定基準になるのである。