1-49-2: ケプラーの法則＜例題＞
楕円軌道の問題は、面積速度一定則と力学的エネルギー保存則を連立させることがカギとなります！
例題
図１には質量\(m\)の人工衛星が、地球の赤道面上を半径\(r\)の円軌道を描きながら周回している様子が示してある。図中のAは円軌道上の１点を指す。人工衛星の円運動の周期を\(T\)として以下の問に答えよ。なお、以下では地球以外の天体からの影響や地球の自転及び公転の影響を無視する。
問１ 万有引力定数と地球の質量との積を求めよ。
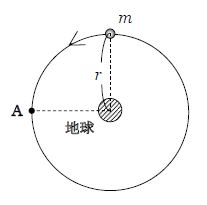
図１の位置Aで、人工衛星が速度の向きを変えずに瞬間的に速さを\(\alpha\)倍（1<\(\alpha<\sqrt{2}\)）に増した。人工衛星は楕円軌道を描きながらやがて地球の中心から最も離れた位置Bに達し、そのときの人工衛星と地球の中心との距離は\(l\)だった。
問２ 位置Bでの人工衛星の速さは、人工衛星が円運動していた時の速さの何倍か答えよ。
問３ 距離\(l\)を\(\alpha\)と\(r\)のみを用いて表せ。
問４ 人工衛星が位置Aから出て再びAに戻ってくるまでの時間は\(T\)の何倍か答えよ。
解答・解説
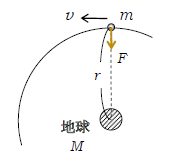
問１ 万有引力定数\(G\)、地球の質量\(M\)、衛星の速さ\(v\)とすると、円運動の方程式(1-20-1)は図２より
\(\displaystyle m\frac{v^2}{r}=F=G\frac{Mm}{r^2}\)
∴ \(\displaystyle v=\sqrt{\frac{GM}{r}}\) (1)
周期(1-19-1) \(\displaystyle T=\frac{2\pi r}{v}=\frac{2\pi}{\sqrt{GM}}r^{\frac{3}{2}}\)
よって \(GM=\) 答 \(\displaystyle 4\pi^2\frac{r^3}{T^2}\)
問２ 図３に楕円軌道を示す。地球から最も近い点を近地点、最も遠い点を遠地点という。動径\(r\)と速度\(\alpha v\)の向きが直交する位置Aは、楕円の性質により近地点・遠地点のみだが、題意より位置Bが遠地点だからAは近地点である。Bでの速さを\(v’\)とし、面積速度一定則(1-49-1)をAとBについて立てると（図３）
A B
\(\displaystyle \frac{1}{2} r\alpha v\sin90^°=\frac{1}{2}lv’\sin90^°\)
(1)を代入して \(\displaystyle \frac{v’}{v}=\) 答 \(\displaystyle \alpha \frac{r}{l}\)
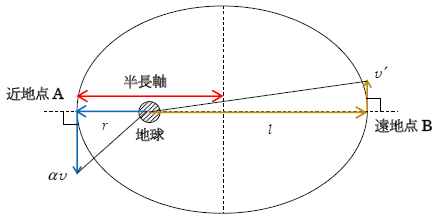
問３ 力学的エネルギー保存則(1-48-1)をAとBについて立てると（図３）
A B
\(\displaystyle \frac{m}{2}(\alpha v)^2+\left(-G\frac{Mm}{r}\right)=\frac{m}{2}v’^2+\left(-G\frac{Mm}{l}\right)\)
まず\(m\)で約分する。さらに、\(GM\)の入った項を右辺に、それ以外の項を左辺に集めるように式変形するのがコツ。
\(\displaystyle \frac{\alpha ^2}{2}v^2-\frac{1}{2}v’^2=GM\left(\frac{1}{r}-\frac{1}{l}\right)\)
問２の答から得られる\(\displaystyle v’=\alpha \frac{r}{l}v\)を代入し、さらに(1)の\(v\)を代入すると
\(\displaystyle \frac{\alpha ^2}{2}\left(1-\frac{r^2}{l^2}\right)\frac{GM}{r}=GM\left(\frac{1}{r}-\frac{1}{l}\right)\)
\(GM\)が約分できて \(\displaystyle \frac{\alpha ^2}{2}\frac{l^2-r^2}{rl^2}=\frac{l-r}{rl}\)
両辺\(\displaystyle \frac{l-r}{rl}\)で割って \(\displaystyle \frac{\alpha ^2}{2}\frac{l+r}{l}=1\)
\(l\)について整理して \((2-\alpha ^2)l=\alpha ^2 r\)
よって \(l=\) 答 \(\displaystyle \frac{\alpha ^2}{2-\alpha ^2}r\)
問４ 位置Aから出て再びAに戻ってくるまでの時間\(T’\)は楕円運動の周期だから、ケプラーの第３法則(1-49-1)を利用する。第３法則を問１の円軌道と問２以降の楕円軌道を比較して立てよう。[ これは言わば、太陽の周りを回る異なる惑星の軌道どうしで第３法則を立てることに相当する。] まず問１の円軌道の半径\(r\)は、円を楕円の一種と見なしたときの半長軸に他ならない。問２以降の楕円軌道の半長軸は図３より\((r+l)/2\)。ケプラーの第３法則は
円 楕円
\(\displaystyle \frac{T^2}{r^3}=\frac{T’^2}{\left(\frac{r+l}{2}\right)^3}\) ∴ \(\displaystyle \frac{T’^2}{T^2}=\left(\frac{r+l}{2r}\right)^3\)
問３の答の\(l\)を代入 \(\displaystyle \frac{T’^2}{T^2}=\left(\frac{r+\frac{\alpha ^2}{2-\alpha ^2}r}{2r}\right)^3=\left(\frac{1}{2-\alpha ^2}\right)^3\)
よって \(\displaystyle \frac{T’}{T}=\) 答 \(\displaystyle \left(\frac{1}{2-\alpha ^2}\right)^{\frac{3}{2}}\)