1-20-1: 円運動の方程式
円運動は半径方向と接線方向に分けて考えるのがコツです!
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ 円運動の方程式(運動方程式の半径方向成分)
中心向きを正として \(\displaystyle ma_中=mr\omega^2=m\frac{v^2}{r} \; =F_中 \)
ここで\(a_中\)は向心加速度、\(F_中\)は向心力(合力の半径方向成分、中心向き正)
・ 運動方程式の接線方向成分
\(\theta\)の増える向きを正として \(\displaystyle ma_接=m\frac{\Delta v}{\Delta t} \)(正確には \(\displaystyle m\frac{dv}{dt}\))\(=F_接 \)
ここで\(F_接\)は合力の接線方向成分
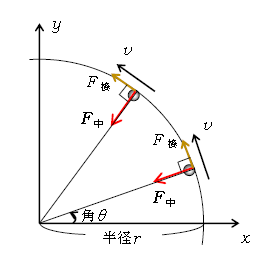
図1はお盆の内側の縁(へり)を小球が円運動していく図。小球に加わる力の半径方向成分(中心向きを正)、接線方向成分(\(\theta\)の増える向きを正)をそれぞれ\(F_中\)、\(F_接\)と図示してあり、ここでは\(F_中\)=お盆から加わる垂直抗力\(N\)、\(F_接\)=動摩擦力\((-f)\)である。\(\theta\)の増える向きを正として\((-f)\)とは、動摩擦力は速度\(v\)と逆向き(図に\(F_接\)と記した向きと逆)に働くという意味。
まず、等速円運動の場合を考えよう。すると、
・ \(F_接\)はない(驚かずに図1の下まで読み進めてほしい)。なぜなら、もし\(F_接\)があると、それは仕事をして小球の運動エネルギー\(\frac{m}{2}v^2 \)を変化させ\(v\)を変えるから、そもそも「等速」円運動ではなくなってしまう。
・ \(F_中\)はある。なぜなら、\(F_中\)と移動の向き(\(v\)の向き、接線方向)は垂直だから、\(F_中 \)は仕事をしない。つまり\(\frac{m}{2}v^2 \)を変えず\(v\)を変えない。しかし、\(F_中\)は進行方向(\(v\)の方向)に対して左向きに加わるから、\(v\)の向きを左へ(円の中心方向へ)と変える。つまり\(F_中\)があるからこそ、軌道は左へ左へ(中心へ中心へ)と曲がっていき、円を描けるのである。
\(F_接\)はないと言ったが、円運動を開始させる直「前」には小球に接線方向の打撃を加えて初速度を与えようとするから、直「前」では\(F_接\)はある。しかし、ひとたび円運動が始まると、(\(F_接\)などなくても)接線方向へ行こうとする速度\(v\)が、\(F_中\)によって中心へ中心へと曲げられながら、円運動が持続していく。
円運動の運動方程式は、向心加速度\(\displaystyle a_中=r\omega^2=\frac{v^2}{r}\)の生じている向きに立てると立てやすい(座標軸\(x\)-\(y\)のことはとりあえず忘れて立てる、と言ってもよい)。
円運動の方程式(運動方程式の半径方向成分):中心向きを正として
\(\displaystyle ma_中=mr\omega^2=m\frac{v^2}{r} \; =F_中 \)
ここで\(F_中\)を向心力という。向心力とは、物体に働く諸々の力(合力)の半径方向成分(中心向き正)のことで、図1では\(N\)である。つまり、向心力は重力、摩擦力、弾性力、・・・のように個別の力に付いた名称ではなく、集合名詞的な語法で合力の中心向き成分のことを指す。
次に、速さの変わっていく非等速円運動について。結論だけを述べると、
向心加速度\(\displaystyle a_中=r\omega^2=\frac{v^2}{r}\) は等速円運動の場合と同様で、したがって円運動の方程式\(\displaystyle ma_中=F_中 \)も全く同じである。
しかし、「非」等速円運動では\(F_接\)がある。\(F_接\)が仕事をして、\(\frac{m}{2}v^2 \)を変化させ、\(v\)を変えるからこそ「非」等速円運動になる。このとき、
\(a_接=\)接線方向の速度\(v\)の単位時間当たりの変化=\(\displaystyle \frac{\Delta v}{\Delta t}\)
[ 正確には \(\displaystyle a_接=\lim_{\Delta t \rightarrow 0} \frac{\Delta v}{\Delta t} =\frac{dv}{dt} \) 微分については1-01-1を参照のこと ]
運動方程式の接線方向成分は、\(\theta\)の増える向きを正として
\(\displaystyle ma_接=m\frac{dv}{dt}=F_接 \) である。


