1-48-3: 静止衛星＜例題＞
万有引力の例題として、静止衛星について考えてみましょう！
静止衛星とは、地球の赤道面上を等速円運動する人工衛星で、地上から見ると１点に静止して見える衛星のこと。立場を逆にして、衛星から見ると、地球の定点（例えば地上から見ている観測者の位置）を見続けることができるので、気象衛星や通信衛星としての目的で用いられる。
静止衛星が静止して見える理由を一言で言うと、
静止衛星の円運動の角速度\(\omega\)=地球の自転の角速度 (1)
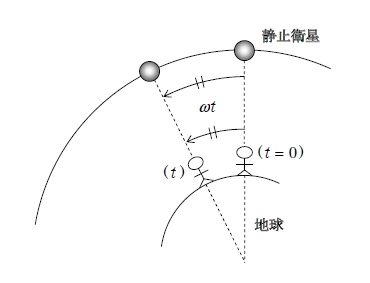
このとき何が起こるかを説明しよう。図１は地球を北極から見たもの。時刻\(t=0\)の瞬間に地球上の観測者の頭上に衛星が位置していたとする。角速度\(\omega\)(1-19-1)とは1sあたり回る角度だから、時間\(t\)の間に衛星は角度\(\omega t\)回る。(1)より同じ時間のあいだに地球及び観測者の回る角度も\(\omega t\)。すると、明らかに時刻\(t\)の瞬間も観測者の頭上に衛星が見えていることになる。ここで\(t\)とはもちろん任意の時間だから、どの時刻\(t\)においても観測者の頭上に衛星は位置し続け、まさに衛星は「静止」して見えるのである。[ なお、今の説明では観測者を赤道面上に置いた（図１）が、例えば緯度40°に位置する観測者からすると、衛星は例えば頭上(天頂)から約40°傾いた南の位置に静止して見える、とだけ言っておく。]
例題
地球の自転の角速度を\(\omega_E\)、地球の半径を\(R\)、重力加速度を\(g\)として、静止衛星の地表面からの高度は\(R\)の何倍か求めよ。
解答・解説
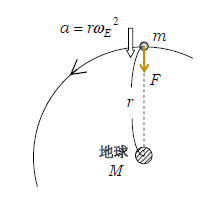
衛星と地球の質量をそれぞれ\(m,M\)、衛星の半径を\(r\)、万有引力定数を\(G\)とすると、図２より円運動の方程式(1-20-1)は
\(\displaystyle mr\omega_E^2=F=G\frac{Mm}{r^2}\) ∴ \(\displaystyle r=\left(\frac{GM}{\omega_E^2}\right)^{\frac{1}{3}}\)
1-48-1で導いた\(GM=gR^2\)の関係式（これは地表での万有引力\(\displaystyle G\frac{Mm}{R^2}=mg\)の関係から導けた）を代入
\(\displaystyle r=\left(\frac{gR^2}{\omega_E^2}\right)^{\frac{1}{3}}\)
地表からの高度\(h=r-R\)
求めるのは \(\displaystyle \frac{h}{R}=\frac{r}{R}-1=\) 答 \(\displaystyle \left(\frac{g}{R\omega_E^2}\right)^{\frac{1}{3}}-1\)
高度\(h\)を具体的に数値計算してみよう。地球は1日＝24時間＝24×60分＝24×60×60s で360°=\(2\pi\) rad回るから、\(\omega_E=2\pi/(24×60×60\text{s})\) 。また\(g≒9.8\:\text{m}/\text{s}\)、\(R≒6.4×10^6\:\text{m}\) 。これらを答に代入すると
\(\displaystyle \frac{h}{R}= \left(\frac{9.8}{6.4}×\left(\frac{2.4×6×6}{2×3.14}\right)^2\right)^{\frac{1}{3}}-1≒5.6\)
つまり、静止衛星の高度は \(h=5.6R≒36000\:\text{km}\) である。