1-48-2: 第１宇宙速度・第２宇宙速度

第１宇宙速度は円運動の方程式、第２宇宙速度は力学的エネルギー保存則を立てましょう！　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

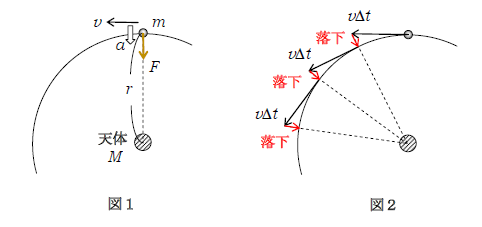
　この単元のタイトル「第１・第２宇宙速度」に取りかかる前に、万有引力の下での代表的な運動 ―― 等速円運動 ―― の説明をしておく。図１には天体(質量\(M\))を中心として、物体(質量\(m\))が半径\(r\)の等速円運動をする様子が示してある。さっそく、運動方程式から始めよう。
　1-19-1の通り、速さ\(v\)は接線方向で、円の中心に向かう向心加速度は\(\displaystyle a=\frac{v^2}{r}\)
　1-48-1の通り、物体に働く万有引力\(F\)は円の中心(天体の中心)に向き、\(\displaystyle F=G\frac{Mm}{r^2}\)
　すると、円運動の方程式(1-20-1)は \(ma=F\) すなわち　\(\displaystyle m\frac{v^2}{r}=G\frac{Mm}{r^2}\)　　(1)
　次に、円運動の周期\(T\)を求めよう。(1)より　\(\displaystyle v=\sqrt{\frac{GM}{r}}\)
　すると1-19-1より　\(\displaystyle T=\frac{2\pi r}{v}=\frac{2\pi}{\sqrt{GM}}r^{\frac{3}{2}}\,\) 　　　　　　　　　　　　　　　(2)

　この周期\(T\)に関して、２つ補足しておく。
1⃣　月の公転周期
　この場合\(M,m\)はそれぞれ地球、月の質量で、地球の半径を\(R\)をとして\(r≒60R\)であることが知られている。
　1-48-1で導いた\(GM=gR^2\)の関係式（これは地表での万有引力\(\displaystyle G\frac{Mm}{R^2}=mg\)の関係から導けた）を(2)に代入すると、
　\(\displaystyle T=\frac{2\pi}{R\sqrt{g}}60R\sqrt{60R}=120\frac{\pi}{\sqrt{g}}\sqrt{60R}\)
　\(\sqrt{g}≒\sqrt{9.8}≒3.1≒\pi\)(単位略)、\(R≒6400\)km\(=6.4×10^6\)ｍ を代入
　\(T=120×\sqrt{60×6.4}×10^3\:\text{s}\)
　\(\sqrt{60}≒7.7\)、\(\sqrt{6.4}≒2.5\)を代入して、1日＝24時間＝24×60分＝24×60×60s であることに注意すると
　\(\displaystyle T=\frac{120×7.7×2.5×10^3\:\text{s}}{24×60×60\:\text{s}/日}=27\:日\)
　これは実際の月の公転周期（詳しくは恒星月）に有効数字2桁で一致する。
　よく言われるのは、ニュートンはリンゴにせよ月にせよ、万有引力の下での宇宙の万物の運動が落下運動であることを看破したということである。例えば（図２）、月は円軌道の接線方向へ速さ\(v\)で動きつつ、万有引力\(F\)に引かれて地球へと落下するから、円運動をするのである。

2⃣　ケプラーの第３法則
　(2)式の両辺を2乗すると　\(\displaystyle \frac{T^2}{r^3}=\frac{4\pi^2}{GM}\)
　これは、周期の2乗と半径の3乗の比が一定値をなすことを意味している。すなわち、ケプラーの第3法則（1-49-1で扱う）の成り立つことが、(楕円運動ではなく)等速円運動という特別の場合に示されたというわけである。

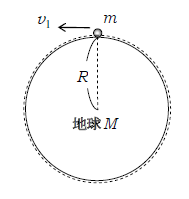
　物体の質量\(m\)、地球の質量\(M\)、地球の半径\(R\)として、円運動の方程式は(1)と同様に
　\(\displaystyle m\frac{v_1^2}{R}=G\frac{Mm}{R^2}\)　　∴　\(\displaystyle v_1=\sqrt{\frac{GM}{R}}\)
　再び1-48-1の関係式\(GM=gR^2\)を代入すると　\(v_1=\sqrt{gR}\)　　　　　　　　 (3)
　数値代入すると　\(v_1=\sqrt{9.8\:\text{m}/\text{s}^2×6.4×10^6\:\text{m}}=7.9\:\text{km}/\text{s}\)
　秒速7.9kmとはずいぶん速いと言えよう。

　次に、第２宇宙速度とは、
　地表から放たれた物体が無限遠へと到達できるための地表での最小速度\(v_2\)　　(☆)
のことである（図４）。ここで、1-48-1の力学的エネルギー保存則
　\(\displaystyle \frac{m}{2}v^2+U=\)一定　　　　　　　　　　　　　　　　　　　　　　　　　　　　(4)
を用いることにする。\(U\)は1-48-1の
　万有引力による位置エネルギー\(\displaystyle U=-G\frac{Mm}{r}\)　　　　　　　　　　　　　　　(5)
である。(5)をグラフにしたものが図５。(4)の右辺は一定値であるが、左辺の位置エネルギー\(U\)は図５より地球の中心からの距離\(r\)とともに単調増大、ということは、左辺の運動エネルギー\(\frac{m}{2}v^2\)は\(r\)とともに単調減少する。

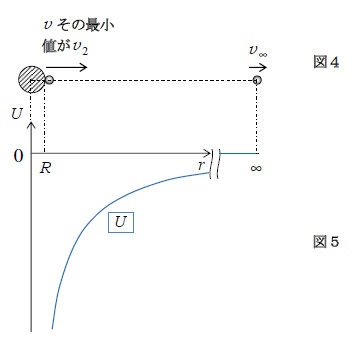
　単調減少してなお無限遠での速さ\(v_{\infty}\)が残っていると仮定して、(4)を立てると、
　　　 地表　　　　　　　　　　　無限遠
　\(\displaystyle \frac{m}{2}v^2+\left(-G\frac{Mm}{R}\right)=\frac{m}{2}v_{\infty}^2+\left(-G\frac{Mm}{\infty}\right)\)　　
　最後の項は\(\frac{1}{\infty}\)が入っているから0である。いま、右辺の\(v_{\infty}\)を小さくしていくと、左辺の地表での速度\(v\)も小さくなる。ゆえに、(☆)で述べた最小速度(第2宇宙速度)\(v=v_2\)となるのは\(v_{\infty}=0\) のときである。
　\(\displaystyle \frac{m}{2}v_2^2+\left(-G\frac{Mm}{R}\right)=\frac{m}{2}0^2+0\)　　∴　\(\displaystyle v_2=\sqrt{\frac{2GM}{R}}\)　
　1-48-1の関係式\(GM=gR^2\)を代入すると　\(v_2=\sqrt{2gR}\;\)　　　　　　　　　 (6)
　数値代入すると　\(v_2=\sqrt{2×9.8\:\text{m}/\text{s}^2×6.4×10^6\:\text{m}}=11.2\:\text{km}/\text{s}\)

（3)と(6)を比べると \(v_2=\sqrt{2}v_1\)　となっている。これを \(\frac{m}{2}v_2^2=2×\frac{m}{2}v_1^2\) として覚えておくのも一法である。
　なお、第２宇宙速度を求める際に、地表面から垂直に物体に初速度\(v_2\)を与えた（図４）。詳しい説明は省略するが、初速度\(v_2\)の向きがたとえ地表面に対して斜めであっても、すなわち物体が曲線軌道を描きながら無限遠に達したとしても、(6)の結論は同じになる。