1-39-1: 剛体のつり合い

ここからしばらく剛体の力学を扱います！　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　剛体とは、簡単に言ってしまえば、固くて変形しない物体のことである。物体を、その質量は考えるが大きさを無視するならば「質点」と呼ぶ。物体を、質点が連続的に広がって分布したものと捉え、どの質点どうしの距離も不変という条件を課す場合は「剛体」と呼ぶ（例えば図１の灰色の物体）。ばねは「弾性体」に分類され、液体・気体は「流体」として扱う。
　1-05-1で力は物体の速度を変化させる原因だと述べた。ということは、力は物体を回転させる原因にもなる。例えば、ドアノブに力を加えればドアは回転軸のまわりに回る。力が物体を回転させる能力を力のモーメントという。モーメントを3次元空間内できっちり数式で表すには、大学の課程「剛体の力学」が必要となるので、この単元では直観的な説明をしていくことにしよう。まず、結論だけ言えば
　モーメント=力×うでの長さ
である。ここで、うでの長さとはこうだ（図１a）。回転中心のことをモーメントの中心という。また、力の加わっている点を力の作用「点」というが、力に沿って平行に引いた線は作用「線」という。モーメントの中心から力の作用線に下した垂線の長さを、うでの長さという。

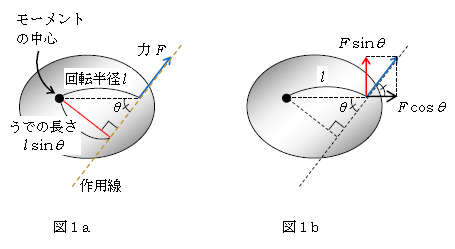
　図１bでは、力\(F\)を回転半径に平行な成分\(F\cos\theta\)と垂直な成分\(F\sin\theta\)に分解してある。
　図１aより、モーメント\(=F\)×うでの長さ\(l\sin\theta=F\sin\theta×l\)
だから、モーメントには力\(F\)のうち回転半径に垂直な成分\(F\sin\theta\)のみが関係し、平行な成分\(F\cos\theta\)は無関係であることが分かる。モーメントの中心を固定して垂直成分\(F\sin\theta\)で引張れば剛体は回転するが、平行成分\(F\cos\theta\)を加えてもビクともしないことから、モーメント(回転させる能力)には垂直成分のみが関わることが容易に分かるだろう。
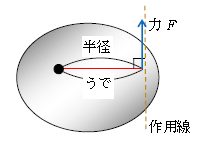
　力と回転半径が垂直な特別の場合は、うでの長さ(モーメントの中心から力の作用線に下した垂線の長さ)は回転半径と等しい（図２）。この場合、モーメント=力×(回転)半径 となる。つまり、半径が大きい方がモーメント(回転させる能力)は大きい。よく経験するように、ドアノブよりもずっと回転軸に近い所を押すとドアを開けづらいのは、半径が小さくてモーメントが小さくなるからだ。ちなみに、半径0となるような点に力を加えても、物体は回転しない（モーメント=力×半径=0である）。

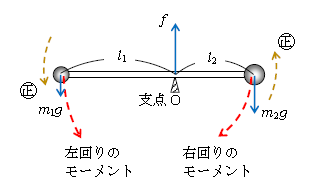
　では図３のように、軽い（質量0と見なせるという意味）太さの無視できる棒を水平にしてその両端に質量\(m_1,m_2\)の小球（大きさを無視して質点扱いするという意味）を取り付けた「剛体」を、支点Oで支える場合を考えてみる。
　重力\(m_1g\)はモーメントの中心Oの回りに棒を左回り(反時計回り)に回転させる能力(モーメント)を持ち、
　左回りのモーメント=力×うで(半径)\(=m_1g×l_1\) 　　(1)
　重力\(m_2g\)は棒を右回り(時計回り)に回転させる能力を持つ。ここで、左回りのモーメントを正に取り、右回りのモーメントを負に取るのが慣習（数学で角度を左回りに測るのにならっている）。
　右回りのモーメント\(=-m_2g×l_2\,\) 　　　　　　　　 (2)
　支点Oから棒に働く力\(f\)は棒を回転させる能力を持たない。なぜなら、 \(f\)はO(モーメントの中心)に加わっているため、うで(半径)が0だから。

　モーメントの合計は(1)＋(2)。これが0になると、棒には回転させる能力が全く加わらないから、棒は回転しなくなる。これをモーメントのつり合いという。すなわち、
　モーメントのつり合い　\(0=m_1gl_1-m_2gl_2\) 　 
　一方、上向きを正にして、力のつり合い　\(0=f-m_1g-m_2g\) 　力がつり合うと、棒は鉛直方向に平行移動（並進運動ともいう）しなくなる。つまり、
　モーメントのつり合いは、回転運動しないための条件　で、
　力のつり合いは、　　　　並進運動しないための条件　である。
回転運動も並進運動もできなければ、剛体(固くて変形しない物体)は完全に静止する。モーメントのつり合いと力のつり合いを連立させることが、剛体のつり合いの条件だ。
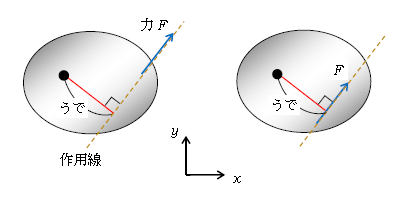
　ここで重要な定理を１つ。「剛体に加わる力は作用線に沿って動かしてもよい」。なぜなら ―― 図４の２つの図を比較すると、力\(F\)を作用線に沿って動かしても、うでの長さは変わらないことが分かる。うでが変わらなければ、モーメントのつり合いの式は変わらない。また、力\(F\)を作用線に沿って動かしても\(F\)の\(x\)成分、\(y\)成分は変わらないから、\(x\)方向、\(y\)方向の力のつり合いの式も変わらない。結局、モーメントも力もつり合いの式は変わらないから、作用線に沿って動かしてもよい ―― これは便利な定理だから、ぜひ活用しよう。
　極端なことを言えば、作用線に沿ってずらしていき、力が剛体の「外に」加わるという現実にはあり得ない状況を想定してもよい。