1-34-1: 束縛条件(張力に伴う条件)

束縛条件という難しく聞こえる用語に惑わされずに、入試の頻出問題をマスターしましょう！　＜続き＞は1-34-2へ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

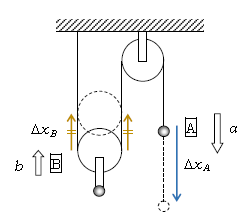
　張力を及ぼすものとしては糸・ひも・綱・ロープなどがあるが、漢字１文字で書けて簡単という理由で、この単元では全て「糸」という語で表す。さっそく図１の動滑車の例で、1-33-1で扱った「束縛条件」（加速度の条件式）を求めてみよう。おもりAが\(\Delta x_A\)下降するとともに、動滑車Bが\(\Delta x_B\)上昇する様子が描かれている。このときA側の糸の長さは青い矢印\(\Delta x_A\)分だけ増え、B側の糸の長さは黄色い矢印\(\Delta x_B\)の２個分だけ減っている。ところで糸の伸び縮みは無視できる。ゆえに糸がピンと張って張力\(T\)が働く場合、AとBは糸の長さが一定のままの運動をする。ということは、増えた分\(\Delta x_A\)と減った分\(2×\Delta x_B\)が等しい。
　　\(\Delta x_A=2\Delta x_B\)
　両辺を時間\(\Delta t\)で割って\(\Delta t\)を限りなく小さくすると
　　\(\displaystyle \lim_{\Delta t \rightarrow 0} \frac{\Delta x_A}{\Delta t}=2\lim_{\Delta t \rightarrow 0} \frac{\Delta x_B}{\Delta t} \)　
　すなわち、速度\(v_A=2v_B\)　（必要なら1-01-1を参照のこと）
　両辺を\(t\)で微分すると　\(\displaystyle \frac{dv_A}{dt}=2\frac{dv_B}{dt}\)　
　すなわち、加速度\(a=2b\)　（必要なら1-02-1を参照）　これが束縛条件である。

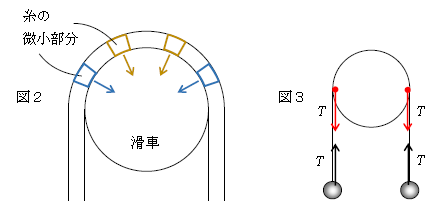
　次の例として、図４のようなおもりA,B,Cと質量の無視できる動滑車Pの運動を考えよう。Pに働く下向きの張力\(T\)が、滑車から糸が離れていく離れ際(図４赤丸)に加わると図示してある。この力の働き方を詳しく書いたのが図２。ピンと張った糸が滑車に巻き付いて、糸の微小部分ごとに滑車を(斜め)下向きに押す。これらの合力を計算してやると実は下向きに\(2T\)になる（具体的な証明は省略するが、例えば積分計算をしてやると\(2T\)になることが示せる）。そこで、1-07-1で述べた糸の性質「(軽い)１本の糸は両端を等しい大きさの力で引っ張る」を用いて、図３のように「滑車から糸が離れていく離れ際(赤丸)に張力\(T\)」と書き込んでやれば事足りるというわけである。図２の糸が滑車を押す力の合計を、図３の糸が滑車を引張る張力で置き換えてやれば、計算上は問題ない。

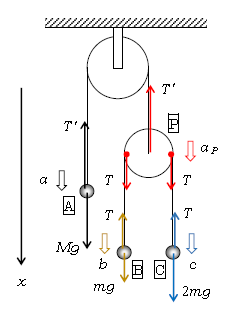
　図４に戻って運動方程式を立てよう。いまおもりA,B,Cの質量がそれぞれ\(M,m,2m\)と文字で与えられているから、下降するのはどのおもりで上昇するのはどれかは分からない。そこで便宜上、下向きを正とする\(x\)軸を取り、正の向きに\(a,b,c,a_P\)とおいた(図示した)。例えば\(a=-\)5のように負の値で求まったなら、実際は上向きに加速するという意味である。決して下向きに加速中という意味ではない。
　A: \(Ma=Mg-T’\)　　　　　(1′)
　B: \(mb=mg-T \, \)　　　　　　(2)
　C: \(2mc=2mg-T\)　　　　　(3)
　P: \(0a_P=2T-T’\)　[ 左辺の0とはPの質量が0(図２の１行下)という意味 ]
　　∴　\(0=2T-T’\)　　∴　\(T’=2T\)　　これを(1′)に代入
　\(Ma=Mg-2T\)　　　　　　 (1)
　この段階で式の数は(1)(2)(3)の3つ、未知数の数は\(a,b,c,a_P,T\)の5つ（\(T’=2T\)と分かっているので\(T’\)は未知数に含めなかった）、ゆえに式の数が２つ足りない。そこで 1⃣ AP間の糸に伴う束縛条件　と 2⃣ BC間の糸に伴う束縛条件　を補おう。
1⃣　AP間の糸は天井に吊った定滑車にかけられている。糸の長さが一定だから、例えばAが3cm下がるとPが等しく3cm上がるというように、AとPの毎秒々々の動き方は(向きは違えど)等しい。ゆえに\(a\)と\(a_P\)は逆向きで大きさが等しく、
　\(a_P=-a\)　　　　　　　　　　 (4′)　[ \(a\)と\(a_P\)は逆符号だから\(a_P=a\)ではない ]
　(4′)は定滑車に伴う束縛条件である。
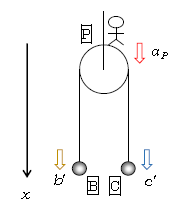
2⃣　BC間の糸は動滑車Pにかけられている。つまり、B,C,P３物体が絡み合いながら動く状況。そこで、図５のようにP上の観測者からB,Cの運動を眺めてみよう。動くP上から見ると、相対加速度が見える。1-30-1の通り「Pから見た」の方で引き算して、Bの相対加速度\(b’=b-a_P\)、Cの相対加速度\(c’=c-a_P\)。ところでタクシーに乗っている人から見ると自分の足元は止まって見えるのと同様に、P上の人から見ると足元のPは止まって見える。こうしてP上の観測者からはPがあたかも定滑車のように見え、1⃣と同様に\(b’\)と\(c’\)は逆向きで大きさが等しくなる。
　∴　\(b’=-c\)　　∴　\(b-a_P=-(c-a_P)\)　　∴　\(b+c-2a_P=0\)
　これが動滑車に伴う束縛条件である。
　(4′)を代入　\(2a+b+c=0 \)　 (4)

　こうして(1)から(4)の4つの式に未知数が\(a,b,c,T\)4つ含まれている状況になり、あとは解くのみである。解き方としては、(1)(2)(3)の運動方程式を質量で割り算して\(a,b,c\)の式をつくり、それを(4)に代入すると\(T\)について解けて、再び(1)(2)(3)に戻してやれば\(a,b,c\)も求まる、とやるのが手早い。
　(1)÷\(M\)　　\(\displaystyle a=g-\frac{2T}{M} \;\:\, \)　　 ①
　(2)÷\(m\)　　\(\displaystyle b=g-\frac{T}{m} \)　　　　②
　(3)÷\(2m\)　 \(\displaystyle c=g-\frac{T}{2m} \)　　　 ③
　(4)に代入　　\(\displaystyle 2\left(g-\frac{2T}{M} \right)+g-\frac{T}{m}+g-\frac{T}{2m}=0 \)
　　∴　\(\displaystyle 4g-\left(\frac{4}{M}+\frac{3}{2m} \right) T=0 \)　　∴　\(\displaystyle \frac{8m+3M}{2Mm} T=4g \)
　∴　\(T=\)\(\displaystyle \frac{8Mm}{3M+8m} g \)　[ 緑の下線は入試でよく聞かれる問題の答という意味 ]　
　①より　\(\displaystyle a=g-\frac{16m}{3M+8m} g= \)\(\displaystyle \frac{3M-8m}{3M+8m} g \)
　②より　\(\displaystyle b=g-\frac{8M}{3M+8m} g= \)\(\displaystyle \frac{-5M+8m}{3M+8m} g \)
　③より　\(\displaystyle c=g-\frac{4M}{3M+8m} g= \)\(\displaystyle \frac{-M+8m}{3M+8m} g \)
　\(a\)の分子に着目すると、\(\displaystyle M>\frac{8}{3} m \)のとき\(a>0\)となることが分かる。\(M\)がある程度大きくなるとおもりAは下向きに加速することが予測されるから、この\(a\)の答は妥当である。