1-33-2: 束縛条件(垂直抗力続き)
1-33-1に引き続いて、動く三角台の理解を深めましょう!
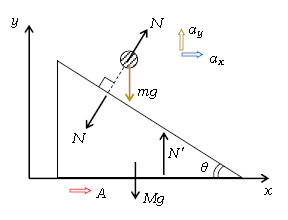
摩擦は全て無視していた。
1-33-1の結果を再掲しておく。
\(N=\)\(\displaystyle \frac{Mm\cos\theta}{M+m\sin^2\theta} g \) (1) \(a_x=\)\(\displaystyle \frac{M\sin\theta\cos\theta}{M+m\sin^2\theta} g \) (2)
\(a_y=\)\(\displaystyle -\frac{(M+m)\sin^2\theta}{M+m\sin^2\theta} g \) (3) \(A=\)\(\displaystyle -\frac{m\sin\theta\cos\theta}{M+m\sin^2\theta} g \) (4)
まず(1)-(4)の吟味(数学的結論の物理的意味を検討する作業)から始めよう。\(M>>m\)の場合どうなるかを調べてみる。このとき\(\displaystyle \frac{m}{M}≒0 \)(無視できる)としてよい。(4)の分母分子を\(M\)で割って
\(\displaystyle A=-\frac{\frac{m}{M}\sin\theta\cos\theta}{1+\frac{m}{M}\sin^2\theta} g≒-\frac{0×\sin\theta\cos\theta}{1+0×\sin^2\theta} g ≒0 \)
この結果は、\(M>>m\)の場合台がひじょうに重くて事実上動けなくなる(固定台になる)ことから妥当である。同様に(1)から
\(\displaystyle N=\frac{m\cos\theta}{1+\frac{m}{M}\sin^2\theta} g ≒m\cos\theta\cdot g=mg\cos\theta \)
この結果も、固定台で\(N=mg\cos\theta \)になることは頻出(1-09-3)で、妥当である。
なお、吟味するとき\(M>>m\)のような極端な状況を考えてみる手法はよく使う。
次に、1-08-1:力学攻略の基本 の運動\(v,x\)を調べる作業に取りかかろう。ここで、
例題
初め小球も三角台も静止していたとする。
問1 球が斜面に沿って距離\(l\)すべるのに要する時間\(t\)を求めよ。
問2 その間の台の変位\(\Delta X\)を求めよ。
解答・解説
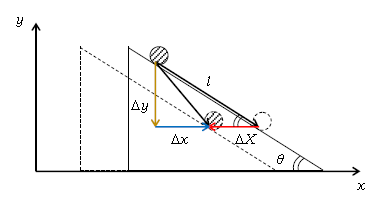
問1 図1のように、\(y\)方向の変位は\(\Delta y=-l\sin\theta \)とすぐ分かるのだが、\(x\)方向の変位\(\Delta x\)は不明。そこで、等加速度の公式を用いて
\(\displaystyle \Delta y=\frac{1}{2}a_y t^2 \) ∴ \(\displaystyle t=\sqrt{\frac{2\Delta y}{a_y} }=\sqrt{\frac{-2l\sin\theta}{a_y} } \)
(2)を代入 \(t=\) 答 \(\displaystyle \sqrt{\frac{M+m\sin^2\theta}{(M+m)\sin\theta} \frac{2l}{g} } \)
問2 等加速度の公式より \(\displaystyle \Delta X=\frac{1}{2}A t^2 \)
(3)と問1の答を代入して \(\displaystyle \Delta X=\frac{1}{2} \left( -\frac{m\sin\theta\cos\theta}{M+m\sin^2\theta} g \right) \frac{M+m\sin^2\theta}{(M+m)\sin\theta} \frac{2l}{g} \)
= 答 \(\displaystyle -\frac{m}{M+m} l\cos\theta \)
→ 束縛条件(張力に伴う条件) は1-34-1へ


