1-23-2: 単振り子の周期

単振り子の周期公式は証明自体が出題されます！　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　単振動の例としてさっそく単振り子の微小振動を扱おう。図１はおもりをつないだ糸が鉛直方向から角度\(\theta\)傾いている状態。(いろいろな記号の書き込みはさておき)図でなめらかな支点を中心に、おもりを円弧にそって左右に往復運動させるのを単振り子という(空気抵抗は無視する)。特にその振れ幅が糸の長さ\(l\)に比べて微小であるときは、単振り子は単振動に帰着する。単振り子の周期の求め方は何通りかある。ここでは代表的な1通りの方法だけを示す。
　図１の\(\theta\)は小さくは図示していないが、振れ幅が微小であるときは、実際には図２のように例えば\(\theta \)≒3° ≒0.0524radとなる。ここで微小角\(\theta\)について成り立つ近似式
　\(|\theta|\)[rad]<<1のとき \(\sin\theta≒\theta≒\tan\theta\) , \(\cos\theta\)≒1　　(1)
を押さえよう。(1)は数学の教科書に載っている(念のため)。\(\theta\)≒3° ≒0.0524radのとき \(\sin\theta\)≒0.0523, \(\tan\theta\)≒0.0524, \(\cos\theta\)≒0.999だから、3°に対しては1/1000の誤差しかない精度の良い近似式であることが分かる。
　図１でおもりの座標\(y=\)糸の長さ\(l-l\cos\theta\) [(1)を用いて] ≒\(l-l×1=0\)
　ということは、単振り子はおもりの上昇分\(y\)を無視できて、\(x\)軸上の直線運動と見なしてよいということである。これは図２を見れば一目瞭然で、円弧が\(x\)軸からせり上がっていく分がほとんど無視できている。

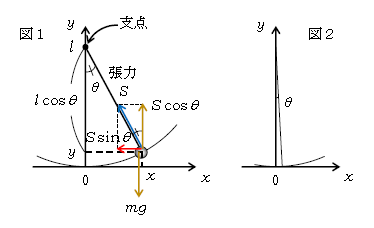
　\(x\)軸上の直線運動だから\(y\)方向はつり合いが成り立ち、図１黄色より
　　\(0=S\cos\theta-mg\)　　∴　\(\displaystyle S=\frac{mg}{\cos\theta}≒mg \)　[(1)を用いた]
　運動方程式の\(x\)成分(図１赤、右向き正)　\(ma=-S\sin\theta=-mg\sin\theta\)
　　[図１より]　\(\displaystyle =-mg\frac{x}{糸の長さl}=-\frac{mg}{l}x \)
　両辺\(m\)で割って　\(\displaystyle (a=)\frac{d^2x}{dt^2} =-\frac{g}{l} (x-0) \)
　これを単振動の方程式　\(\displaystyle \frac{d^2x}{dt^2} =-\omega^2 (x-x_c) \)　と比べることにより
　\(\omega\) \(\displaystyle =\sqrt{\frac{g}{l}} \) 、 \(x_c\) \(=0\) 　　　　　　　　　　　　　　　(2)
と読み取れる。そう、単振り子は\(x\)軸上の単振動なのである（1-18-1図４参照）。少し補足をしておくと、加速度\(\displaystyle a=\frac{d^2x}{dt^2} \)は1sあたりの速度の変化だから、平たく言うなら速くなったり遅くなったりの様子を定める量。加速度が定数なら等加速度運動。一方、加速度\(\displaystyle \frac{d^2x}{dt^2} =-\omega^2 (x-x_c) \)の形（これは1-22-1でやった通り単振動の定義式である）になったら、単振動である証拠なのだ。あとは(2)の\(\omega\)を1-23-1の周期公式\(\displaystyle T=\frac{2\pi}{\omega} \)に代入して
　周期\(\displaystyle T=2\pi\sqrt{\frac{l}{g}} \)
　\(T=2\pi \sqrt{\frac{l}{g}} \)は問題文で「導出せよ」と言われない限り断りなく使ってよい公式で、出題率も極めて高いから、ぜひ覚えておきたい。分子の\(l\)を「リン」と読み、分母の\(g\)を「ゴ」と読んで、「リンゴの公式」と言ったりもする（昭和の頃からあるネーミングのようだ）。