1-15-2: 放物運動（続き）

放物運動の頻出の計算例をしっかりマスターしましょう！　→　1-15-3へ続く　　　　　　　　　　　　　　　　　　　　　　　　

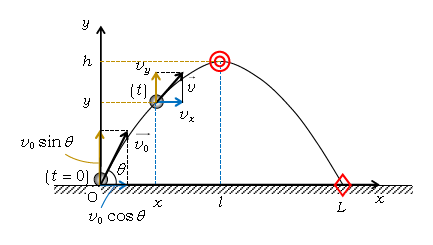
　1-15-1の図を図１として再掲した。これを題材に、入試でよく扱われる以下の量を求めていこう。なお、速度の$x$成分は1-15-1の通り$v_0\cos\theta$のまま一定だから扱わない。また、$a_x=0$、$a_y=-g$である。
　最高点（図１の◎印）での時刻$t_1$、$v_y$ 、$x=l$、$y=h$
　最高点では、1-04-1の通り$v_y=0$ 。つまり、上昇速度$v_y=0$になると、まさにそれ以上上昇しなくなり、最高点に達する。
　すると等加速度の公式$v=v_0+at$ の$y$成分バージョン$v_y=v_{0y}+a_y t$ により、
　　$\displaystyle$$v_y=0=v_0\sin\theta-gt_1$　　∴　$t_1=$ $\displaystyle \frac{v_0}{g} \sin\theta$
　　[ 緑の下線は、入試問題でよく聞かれる問題の答という意味 ]
　等加速度の公式$x=x_0+v_0 t+\frac{1}{2}at^2$の$x$成分バージョン$x=x_0+v_{0x} t+\frac{1}{2}a_x t^2$より、
　　$\displaystyle$$\displaystyle x=l=0+v_0\cos\theta \cdot t_1+0=v_0\cos\theta \cdot \frac{v_0}{g} \sin\theta =$$\displaystyle \frac{v_0^2}{g} \sin\theta\cos\theta$
　$y$成分バージョン$y=y_0+v_{0y} t+\frac{1}{2}a_y t^2$より、
　　$\displaystyle y=h=0+v_0\sin\theta \cdot t_1-\frac{1}{2}gt_1^2=v_0\sin\theta \cdot \frac{v_0}{g} \sin\theta-\frac{1}{2}g \left(\frac{v_0}{g} \sin\theta \right)^2$
　　$\displaystyle =\left(1-\frac{1}{2} \right)\frac{v_0^2}{g} \sin^2\theta=$ $\displaystyle \frac{v_0^2}{2g} \sin^2\theta$

　落下点（図１の◇印）での時刻$t_2$、$v_y$ 、$x=L$
　落下点では明らかに$y=0$
　すると$\displaystyle y=0=y_0+v_{0y} t+\frac{1}{2}a_y t^2=0+v_0\sin\theta \cdot t_2-\frac{1}{2}gt_2^2$
　これは$t_2$に関する２次方程式で、変形すると　$\displaystyle t_2 \left(\frac{1}{2}gt_2-v_0\sin\theta \right)=0$
　　∴　$t_2=0、$ $\displaystyle \frac{2v_0}{g}\sin\theta$　[ ２次方程式なので解が２つ求まるが、$t=0$の解は小球の投げ出し時刻で$y=0$になっているという意味なので、解としては不適 ]
　ちなみに$t_2=2t_1$になった。この意味の考察は次の単元1-15-3でやる。
　次に$\displaystyle v_y=v_{0y}+a_y t=v_0\sin\theta-gt_2=v_0\sin\theta-g\frac{2v_0}{g}\sin\theta=$ $-v_0\sin\theta$
　これが初速度の$y$成分$v_0\sin\theta$の(-1)倍になっている意味の考察も1-15-3で。
　$\displaystyle x=L=x_0+v_{0x} t+\frac{1}{2}a_x t^2=0+v_0\cos\theta \cdot t_2+0$
　　$\displaystyle =v_0\cos\theta \cdot \frac{2v_0}{g} \sin\theta=\frac{v_0^2}{g}2\sin\theta\cos\theta=$$\displaystyle \frac{v_0^2}{g}\sin2\theta$　
　[ 倍角の公式を用いた ]　

　初速度の大きさ$v_0$を一定に保ったまま、投げ出しの角$\theta$を10°,23°,84°のようにいろいろ変えていったときの$L$の最大値、つまり水平方向の到達距離の最大値、およびそのときの$\theta$
　で求めた$\displaystyle L=\frac{v_0^2}{g}\sin2\theta$で、$\theta$を変数と見なして$L$の最大値を求めるというもの。
　-1≦$\sin2\theta$≦1だから、$\displaystyle L_{\text{max}}=\frac{v_0^2}{g} (\sin2\theta)_{\text{max}} =\frac{v_0^2}{g}×1=$ $\displaystyle \frac{v_0^2}{g}$
　また、$\sin2\theta$が最大値1をとるのは$\sin$の中身$2\theta=90°$のときだから、$\theta=$ $45°$。
　低すぎる角度(例えば15°)で投げても、高すぎる角度(例えば75°)で投げても、$L$は大きい値にはならないが、程よい角45°で投げると最も遠くへ到達するという意味。

　軌跡の式
　軌跡の式とは$x$-$y$平面における関数関係$y=f(x)$を曲線表示したもの。次のようにして求める。
　$x$と$t$ の関係式　$x=v_0\cos\theta \cdot t$　　　　　　(1)
　$y$と$t$ の関係式　$\displaystyle y=v_0\sin\theta \cdot t-\frac{1}{2}gt^2$　　(2)
から$t$を消去すれば、関数$y=f(x)$が得られて、それが軌跡の式になる。
　そこで(1)より得られる $\displaystyle t=\frac{x}{v_0\cos\theta}$ を(2)に代入して$t$を消去する。
　　$\displaystyle y=v_0\sin\theta \frac{x}{v_0\cos\theta}-\frac{1}{2}g \left(\frac{x}{v_0\cos\theta} \right)^2$
　　∴　$\displaystyle y=\tan\theta \cdot x-\frac{g}{2v_0^2\cos^2\theta}x^2$
　これは$x$の2次の係数が負の2次関数だから、上に凸の放物線で、たしかに小球を空中に投げ出すと放物線を描く（図１）。
　ちなみに2次関数を平方完成すると、
　　$\displaystyle y=-\frac{g}{2v_0^2\cos^2\theta} \left( x^2-\frac{2v_0^2\cos^2\theta}{g}\tan\theta \cdot x \right)$
　　$\displaystyle =-\frac{g}{2v_0^2\cos^2\theta} \left(x^2- \frac{2v_0^2}{g}\sin\theta\cos\theta \cdot x \right)$
　　$\displaystyle =-\frac{g}{2v_0^2\cos^2\theta} \left(x- \frac{v_0^2}{g}\sin\theta\cos\theta \right)^2+\frac{g}{2v_0^2\cos^2\theta} \left( \frac{v_0^2}{g}\sin\theta\cos\theta \right)^2$
　∴　$\displaystyle y=-\frac{g}{2v_0^2\cos^2\theta} \left( x- \frac{v_0^2}{g}\sin\theta\cos\theta \right)^2 +\frac{v_0^2}{2g}\sin^2\theta$
　これから軸$\displaystyle x=\frac{v_0^2}{g}\sin\theta\cos\theta$、頂点の$\displaystyle y=\frac{v_0^2}{2g}\sin^2\theta$であることが分かる。軸及び頂点はで求めた$x=l$、$y=h$に一致している。