1-02-2: v-tグラフ ＜例題＞

問題を実際に解いてみることは、理解を深めるための絶好のチャンスです！　　　　　　　　　　　　　　　　　　

例題　

　時刻\(t=0\)に出発して一直線上を運動する物体がある。出発点を原点とし、物体の運動方向に沿って\(x\)軸を取る。図１のグラフは、物体の速度\(v\)と時間\(t\)の関係を示したものである。
問１　物体の加速度\(a\)と時間\(t\)の関係をグラフに表せ。
問２　時刻 \(t=0\)から\(t=4t_0\)までの物体の変位を求めよ。
問３　物体の位置\(x\)と時間\(t\)の関係をグラフに表せ。

解答・解説

問１　1-02-1の通り、加速度\(a=v\)-\(t\)グラフの傾き 
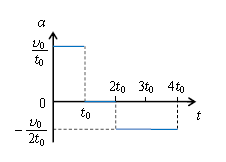
　図１で\(0～t_0\)では　\(\displaystyle a=\frac{タテの変化v_0}{ヨコの変化t_0} =\frac{v_0}{t_0}\)　これを図２の縦軸\(a\)に取る。
　　　　\(t_0～2t_0\)では　\(\displaystyle a=\frac{タテの変化0}{ヨコの変化t_0} =0\)
　　　　\(2t_0～4t_0\)では　\(\displaystyle a=\frac{タテ-v_0}{ヨコ2t_0} =-\frac{v_0}{2t_0}\)
　よって、以下の図２が　答　　

問２　1-02-1の通り、変位\(v\)-\(t\)グラフの面積
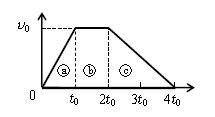
　図３は図1にⓐ、ⓑ、©の記号を割り当てたものである。
　\(4t_0\)までの変位=(ⓐ＋ⓑ+©)の台形の面積
　　　　　　　＝\(\displaystyle (t_0+4t_0)\times v_0\div 2=\frac{5}{2} v_0t_0\)
　答　 \(\displaystyle \frac{5}{2} v_0t_0\)

問３　\(t_0\)までの変位= 図３ⓐ= \(\displaystyle t_0\times v_0\div 2=\frac{1}{2} v_0t_0\)　これを図４の縦軸に取る。　
　　　\(2t_0\)までの変位=ⓐ＋ⓑ= \(\displaystyle (t_0+2t_0)\times v_0\div 2=
\frac{3}{2} v_0t_0\)　
　　　\(4t_0\)までの変位= \(\displaystyle \frac{5}{2} v_0t_0\)　は問２で既に求めた。
　ところで1-01-1の通り、\(x\)-\(t\)グラフの接線の傾き=速度\(v\) であることに注意すると、図４が書ける。
　図４のd:　\(0～t_0\)では図２より\(v\)が増えるから、\(x\)-\(t\)グラフの接線の傾きが増えていく　
　　　　e:　\(t_0～2t_0\)では\(v\)一定だから\(x\)-\(t\)グラフの傾き一定　
　　　　f:　 \(2t_0～4t_0\)では速度\(v\)が減るから\(x\)-\(t\)グラフの接線の傾きが減っていく　　
　よって図４が　答