1-31-3: 運動量保存則 <例題2>(1次元衝突)
1-31-2の例題1の続き。計算力の付く問題です!
例題2
問4 衝突前後のAとBの運動エネルギーの減少量を求めよ。 [ この問4は計算が少々面倒なので、先に答を見てから、あらためて自分でやり直すこともおすすめです ]
解答・解説
衝突後のA、Bの速度(1-31-2問1の答)及び1-31-2の図1を再掲しておく。
A: \(\displaystyle v=\frac{m-eM}{m+M}v_0 \) 、 B: \(\displaystyle V=\frac{(1+e)m}{m+M}v_0\)
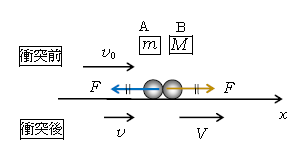
問4 運動エネルギーの減少量とは、衝突前の運動エネルギーから衝突後のそれを引いたもの。
求める減少量(図1より)=\(\displaystyle \frac{m}{2}v_0^2-\left( \frac{m}{2}v^2+\frac{M}{2}V^2 \right) \)
\(\displaystyle =\frac{m}{2}v_0^2-\left( \frac{m}{2} \left( \frac{m-eM}{m+M}v_0 \right)^2 + \frac{M}{2} \left( \frac{(1+e)m}{m+M}v_0 \right)^2 \right) \)
< 第1,2,3項全てから\(\displaystyle \frac{m}{2}v_0^2 \)が括り出せる。さらに分母\((m+M)^2\)で通分して >
\(\displaystyle =\frac{\frac{m}{2}v_0^2}{(m+M)^2}[(m+M)^2-(m-eM)^2-(1+e)^2mM] \) (☆)
いま [ ]の中身
\(=m^2+2mM+M^2-m^2+2emM-e^2M^2-mM-2emM-e^2mM \)
< \(m^2\)と\(-m^2\)がキャンセル。\(2emM\)と\(-2emM\)もキャンセル。\(2mM\)と\(-mM\)合わせて\(mM\) >
\(=mM+M^2-e^2M^2-e^2mM=mM+M^2-e^2(mM+M^2) \)
\(=(1-e^2)(mM+M^2)=(1-e^2)M(m+M) \)
これを(☆)の [ ]の中に代入
減少量\(\displaystyle =\frac{\frac{m}{2}v_0^2}{(m+M)^2} (1-e^2)M(m+M) \)
よって 答 \(\displaystyle (1-e^2)\frac{m}{2}v_0^2 \frac{M}{m+M} \)
これから分かることは、
\(e=1\) 弾性衝突では、減少量が0、つまり運動エネルギーは保存する。
\(0≦e<1 \, \) 非弾性衝突では、減少量が>0、 運動エネルギーは減少する。
これは、今の例題のように衝突前Bが静止している場合だけでなく、運動している場合も一般的に成り立つことである(一般的な場合の証明は省略)。結局、非弾性衝突では、衝突時に発生する熱エネルギーなどの形で運動エネルギーが失われてしまう。したがって、非弾性衝突で力学的エネルギー保存則を用いることはできない。


