1-19-1: 等速円運動
円運動の速度・加速度は、時間を限りなく小さく取るイメージが大事。図を参考にしましょう!
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
角速度(1sあたり回る角)\(\omega \)、円の半径\(r\)として、等速円運動の
・ 速度\(\vec{v}\) 接線方向 \(v=r\omega \)
・ 加速度\(\vec{a}\) 中心を向く向き \(\displaystyle a=r\omega^2=\frac{v^2}{r} \)
この加速度をとくに向心加速度という
・ 周期
\(\displaystyle T=\frac{2\pi r}{v}=\frac{2\pi}{\omega}\)
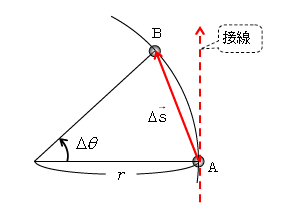
等速円運動とは、文字通り「速さ一定のまま円を描く運動」のこと。これからその基本量1⃣2⃣3⃣について説明していく。図1には物体が半径\(r\)の円を描きながら、点AからBへ中心角\(\Delta \theta \)回り、\(\Delta\vec{s} \)だけ変位していく様子が示されている。
1⃣ 角速度\(\omega \)(ギリシャ文字のオメガ。アルファベットのwではない。念のため)とは、1sあたり回る角度。
\(\displaystyle \omega=\frac{\Delta \theta}{\Delta t} \) (1)
[ 正確には \(\displaystyle \omega=\lim_{\Delta t → 0} \frac{\Delta \theta}{\Delta t} =\frac{d\theta}{dt} \) 微分については1-01-1を参照のこと ]
\(\displaystyle \)\(\omega \)の単位は[rad/s]。ただし、1radとは半径1個分の弧長を張る中心角のことだから、○○radとは要は半径○○個という意味。1個、3個、…などは通常は単位と見なされないので、\(\omega \)の単位は実質上[1/s]である。ただし、[1/s]と書いてしまうと角度を[rad]で測っているのか[°]で測っているのか不明だから[rad/s](場合によっては[°/s])と書く。
2⃣ 速度\(\displaystyle \vec{v}=\frac{変位\Delta\vec{s} }{\Delta t} \) [ 正確には \(\displaystyle \vec{v}=\lim_{\Delta t → 0} \frac{\Delta\vec{s} }{\Delta t} =\frac{d\vec{s} }{dt} \) ]
ということは、速度\(\vec{v}\)の向きは\(\Delta \vec{s} \)の向きに等しい。図1で\(\Delta t → 0\)とすると\(\Delta \theta → 0\)となり、B→Aに限りなく近づくから、速度\(\vec{v}\)の向き(\(\Delta \vec{s} \)の向き)は接線方向に一致すると分かる。
次に、速度の大きさ(速さ) \(\displaystyle v=|\vec{v}|=\frac{|\Delta\vec{s}| }{\Delta t}=\frac{弦\text{AB} }{\Delta t}=\frac{弧\text{AB}}{\Delta t} \)
[\(\Delta t → 0 \)としているので弦も弧も等しい ] \(\displaystyle=\frac{r\Delta \theta}{\Delta t}=r\omega \) [ (1)を代入した ]
∴ \(v=r\omega \) (2)
角速度\(\omega \)とは、1sあたり何rad回るか、すなわち1sあたり半径何個分の弧長を描くかであるから、
速さ\(v\)=1sあたりの移動距離=半径\(r\)×1sあたり半径\(\omega \)個分の弧長=\(r\omega \) となるのは当然である。
3⃣ 加速度\(\displaystyle \vec{a}=\frac{速度変化\Delta\vec{v} }{\Delta t} \) [ 正確には \(\displaystyle \vec{a}=\lim_{\Delta t → 0} \frac{\Delta\vec{v} }{\Delta t} =\frac{d\vec{v} }{dt} \) ]
ということは、加速度\(\vec{a}\)の向きは\(\Delta \vec{v} \)の向きに等しい。図2に等速円運動する物体のある瞬間の速度\(\vec{v}\)、\(\Delta t\)後の速度\(\vec{u}\)が示してある。一方、図3は図2の\(\vec{v}\)と\(\vec{u}\)を平行移動して、それらの始点を付けた図。例えば図2で\(\vec{v}\)と\(\vec{u}\)が90°をなすとすると、図3の\(\vec{v}\)と\(\vec{u}\)も90°をなすことから分かる通り、図2と図3の中心角はともに\(\Delta \theta \)で等しい。速度変化\(\Delta\vec{v} =\)あと\(\vec{u}-\)まえ\(\vec{v}\) だから、図3のPQに向くベクトルががまさに\(\Delta\vec{v} \)である。
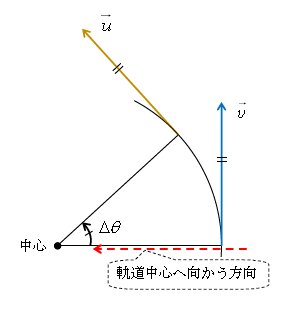
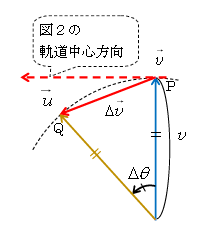
図3で\(\Delta t → 0\)とすると\(\Delta \theta → 0\)となり、Q→Pに限りなく近づくから、加速度\(\vec{a}\)の向き(\(\Delta\vec{v} \)の向き)は(円)軌道の中心方向に一致すると分かる。図2で上を向いた速度\(\vec{v}\)が、わずかな時間経つとごく少しだけ左に傾いた\(\vec{u}\)に変化する、その左向きが速度の変化していく向き(加速度の向き)であって、だから加速度は中心方向というわけである。この加速度をとくに向心加速度という。
次に、加速度の大きさ \(\displaystyle a=|\vec{a}|=\frac{|\Delta\vec{v}| }{\Delta t}=\frac{弦\text{PQ} }{\Delta t}=\frac{弧\text{PQ}}{\Delta t} \)
[ 図3で 弧\(\text{PQ}=\)半径\(v×\Delta \theta \) に注意すると ] \(\displaystyle=\frac{v\Delta \theta}{\Delta t}=v\omega\) [ (2)を代入して ]
\(=r\omega \cdot \omega =r\omega^2 \) さらに \(\displaystyle =\frac{(r\omega)^2}{r} =\frac{v^2}{r} \)
∴ \(\displaystyle a=r\omega^2=\frac{v^2}{r} \) (3)
(2)のすぐ下に\(v=r\omega \)の直観的な理解の仕方を書いたが、(3)については直観的にすぐ1行で言えるような理解の仕方はない。むしろ(3)は単位とともに覚えておくのがよい。ついでに(2)もである。
\(\displaystyle a = r\omega^2 = \frac{v^2}{r} \) 、 \(v = r\omega \)
[ \(\text{m}/\text{s}^2 \) = \(\text{m}(1/\text{s})^2 \)= \(\displaystyle \frac{(\text{m}/\text{s})^2}{\text{m}} \) ] [ \(\text{m}/\text{s} \) = \(\text{m}(1/\text{s}) \) ]
最後に4⃣として周期\(T\)を扱っておこう。周期とは物体が円1周を描くに要する時間のこと。よって
周期=円周÷速さ=1周の角度\(2\pi\)÷1sあたり回る角
\(T\) \(=\) \(\displaystyle \frac{2\pi r}{v}\) \(=\) \(\displaystyle \frac{2\pi}{\omega}\) となる。


