1-07-2: 運動方程式の立て方 ＜例題＞

1-07-1に引き続き、力を図示し、運動方程式を立てる練習をしましょう！　　　　　　　　　　　　　　　　　

例題　

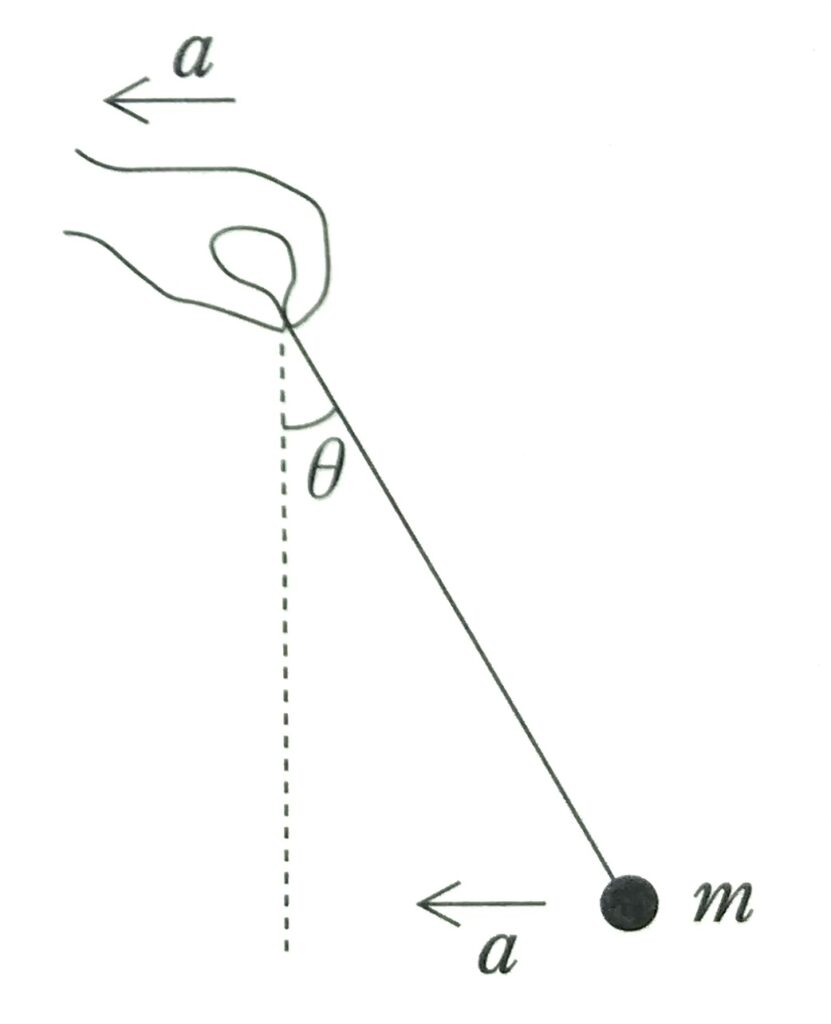
　図のように、質量\(m\)のおもりがつり下げられた糸の上端を手で持ち、糸の傾きを一定に保ちながらおもりを水平方向に直線運動させる。糸が鉛直となす角度を\(\theta \)とするとき、おもりの加速度の大きさ\(a\)として正しいものを、下の①～⑧のうちから一つ選べ。ただし、重力加速度の大きさを\(g\)とする。
①　\(g\sin\theta \)　　②　\(mg\sin\theta \)　　③　\(g\tan\theta \)　　④　\(mg\tan\theta \)　
⑤　\(\displaystyle \frac{g}{\cos\theta} \)　　⑥　\(\displaystyle \frac{mg}{\cos\theta} \)　　⑦　\(\displaystyle \frac{g}{\tan\theta} \)　　⑧　\(\displaystyle \frac{mg}{\cos\theta} \)　

解答・解説

　問題文には座標軸が書かれていないが、座標軸（とりわけその正の向き）を決めておかないと、加速度がプラスなのかマイナスなのか表現しようがない、つまり運動方程式が立てようがないから、自分で座標軸の正の向きを書き込んでおく（図１）。おもりは水平左向きに動いているので、その直線運動の向きに\(x\)軸を取り、垂直な方向に\(y\)軸を取るとよい。
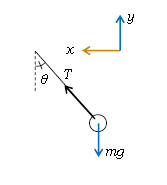
　まず力　「注目物体」をおもりに取る。
１．重力を書く、\(mg\)。
２．ふれているものを探す（接触力）。おもりに糸がふれているから、1-07-1の通り「糸と平行、おもりを引っ張る向き」に張力\(T\)と書く。
　力はこれで終わり。

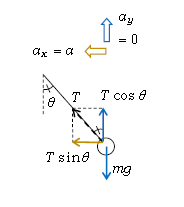
　次に\(ma=F\)　\(x\)方向、\(y\)方向の加速度を、それぞれの正の向きに\(a_x=a\)、\(a_y=0\)と図示する（図２）（おもりは水平左向きに動いている、つまり\(y\)方向には動いていないので\(a_y=0\)）。
　さらには、座標軸に対して斜めの力を\(x\)成分、\(y\)成分に分解しておこう（力は向きと大きさを持ついわゆるベクトルで、それを成分に分解するという意味）。斜めの\(T\)を分解するには、\(T\)を対角線に持ち\(x\)軸、\(y\)軸に平行な長方形を書けばよい（図２）。\(x\)成分は\(T\sin\theta \)、\(y\)成分は\(T\cos\theta \) 。一方、\(y\)軸に平行な\(mg\)は分解しない。

　運動方程式は各方向ごとに別々に立てる。我々の宇宙は、運動方程式が\(x\)方向、\(y\)方向別々に成り立つようにできているからである。
　まず\(x\)方向に加わる力だけをかき集めて合力(力の合計)の\(x\)成分\(F_x\)を計算し、\(x\)方向の運動方程式\(ma_x=F_x\)を立てる。正の向きと照らし合わせながら力の符号を正しく入れていくこと。図２より\(F_x=T\sin\theta \)だから、
　　\(ma=T\sin\theta \)　　　　 (1)
　次に\(y\)方向の力だけをかき集めて合力の\(y\)成分\(F_y\)を計算し、\(y\)方向の運動方程式\(ma_y=F_y\)を立てる。\(F_y=T\cos\theta -mg \)だから、\(ma_y=m0=T\cos\theta -mg\) つまり
　　\(0=T\cos\theta -mg \)　　(2)　（(2)は\(y\)方向のつり合いの式に他ならない）
　(1)、(2)は\(a\)と\(T\)を未知数とする連立方程式。
　(2)より　\(\displaystyle T=\frac{mg}{\cos\theta} \)　
　(1)に代入　\(\displaystyle ma=\frac{mg}{\cos\theta} \sin\theta=mg\tan\theta \)　　∴　\(a =g\tan\theta\)
　答　③