1-04-2: 落体の運動 ＜例題＞

1-04-1に引き続き、計算のコツをつかんで行きましょう！　　　　　　　　　　　　　　　　　　　　　　　

例題　

　地上で、ある物体を鉛直方向に投げ上げた。このとき、物体の高さ\(y\)と時刻\(t\)の関係は、図１に示すグラフのようになった。ただし、図１のグラフの横軸の1目盛りは1秒である。縦軸の1目盛りの大きさは記入していない。

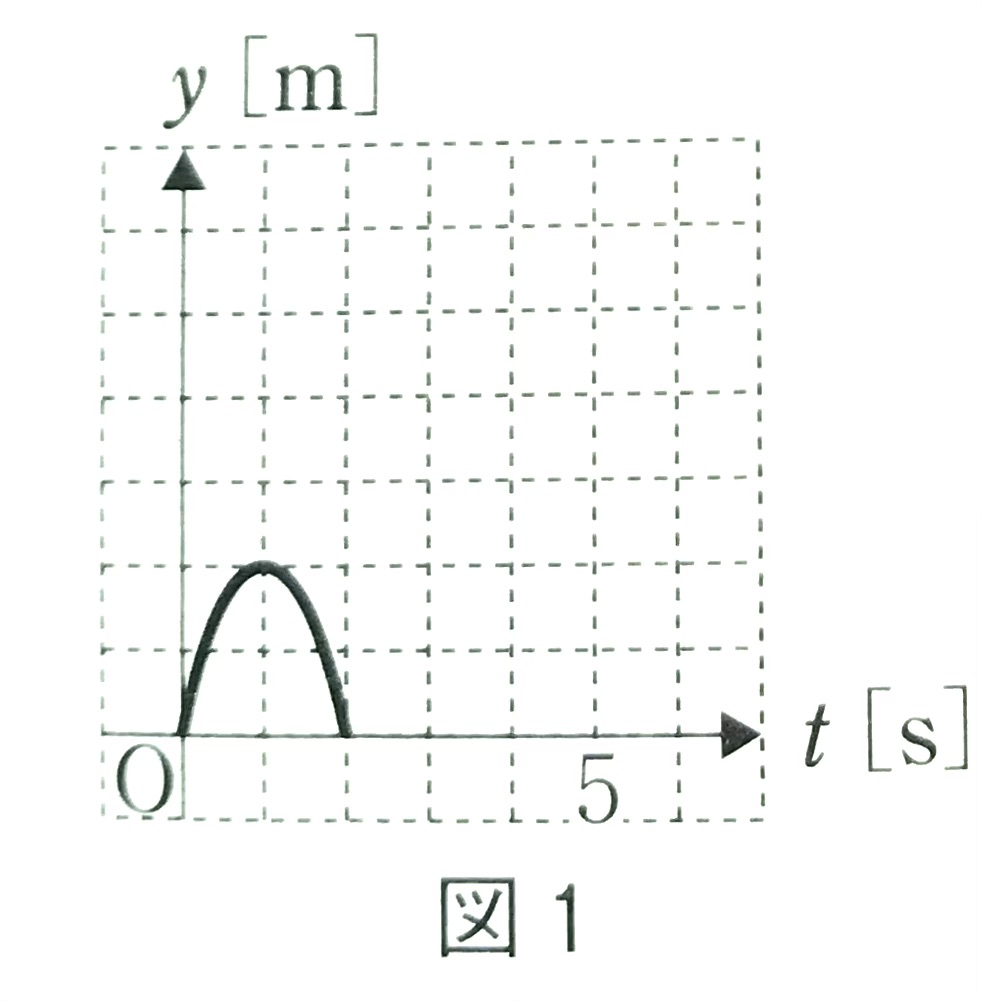
問１　最高点の高さはいくらか。最も適当な数値を、次の①～⑤のうちから一つ選べ。ただし、重力加速度の大きさを9.8m/s\(^2\)とする。
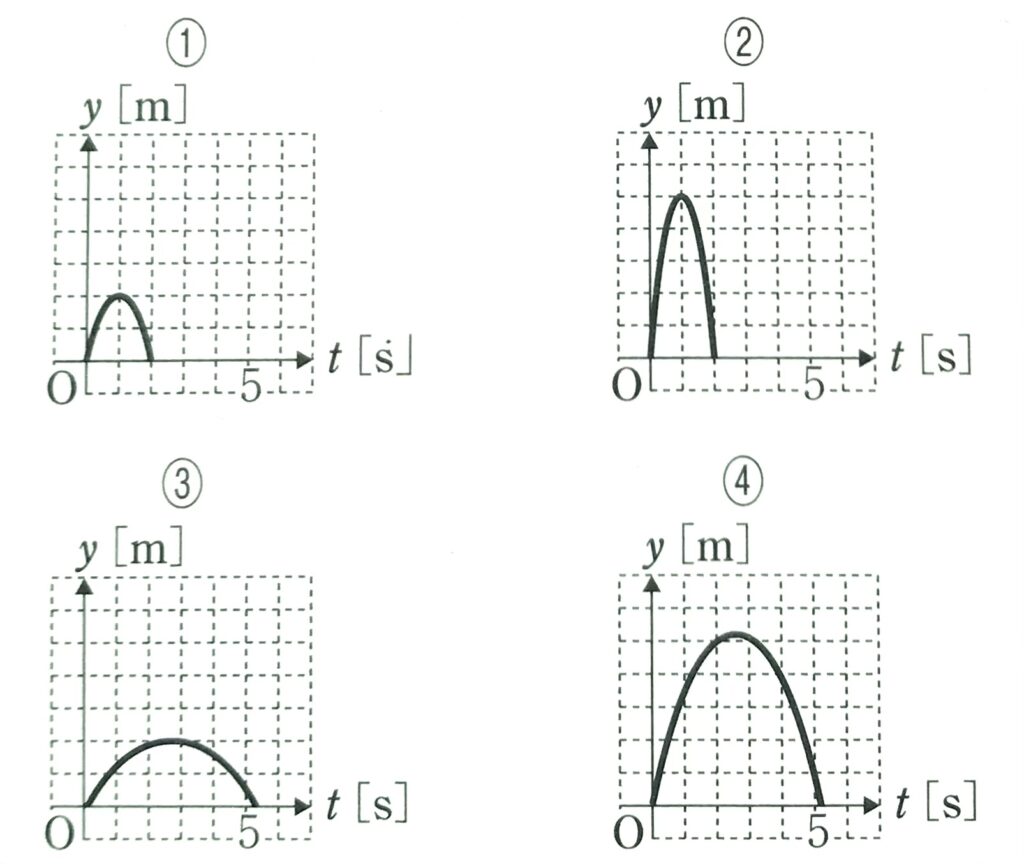
問２　火星上の重力加速度の大きさはおよそ3.7m/s\(^2\)である。火星上で、同じ物体を、同じ初速度で鉛直方向に投げ上げたとき、その運動を表すグラフはどのようになるか。最も適当なものを、次の①～④のうちから一つ選べ。ただし、グラフの1目盛りは図１と同じものとする。

解答・解説

問１　最高点に達する時刻を\(t_1\)とすると、\(t_1\)は図１の横軸1目盛りめで、問題文に「横軸の1目盛りは1s」とあるから\(t_1=\)1s
　最高点では1-04-1の通り　\(v=0=v_0-gt_1=v_0-\)9.8×1　　
　　∴　\(v_0=\)9.8m/s　　　　(1)
　最高点の高さ\(h\)とすると、1-04-1の通り　\(\displaystyle h=0+v_0t_1-\frac{1}{2} gt_1^{\;2} \)
　　　[ 右辺第1項の0は初期位置が0の高さという意味 ]
　　\(=\)9.8×1\(\displaystyle -\frac{1}{2}\)×9.8×1\(^2=\)4.9m　　　
　答　③　　この4.9mは図１の縦軸約2目盛りだから、縦軸1目盛りは約2.5mであると考えられる ―― (a)　　　　　　　　　　　　　　　　　　　　　　　　　　

問２　正しいグラフを選ぶには、火星で最高点に達する時刻(\({t_1}’\)とする)や、火星での最高点の高さ(\(h’\)とする)が分からなければならないだろう。火星の重力加速度を\(g’\)とすると、問題文に「同じ初速度」とあるから、
　最高点では　\(v=0=v_0-g'{t_1}’\)
　　∴　\(\displaystyle {t_1}’=\frac{v_0}{g’}\)　　　　　　(2)
　問題文に\(g’=\)「3.7m/s\(^2\)」とあり、また(1)も代入すると
　　\(\displaystyle {t_1}’=\frac{9.8}{3.7} \)≒ 2.6s　つまり横軸約2.6目盛りの時刻 ―― (b)　　　　　　
　最高点の高さ\(\displaystyle h’=0+v_0{t_1}’-\frac{1}{2} g'{{t_1}’}^2 \)　[ (2)を代入 ]
　　\(\displaystyle =v_0\frac{v_0}{g’} -\frac{1}{2} g’ \left( \frac{v_0}{g’} \right)^2=\frac{{v_0}^2}{2g’} =\frac{9.8×9.8}{2×3.7} \)≒ 13m
　これは(a)より、縦軸約\(\displaystyle \frac{13\text{m}}{2.5\text{m}}= \)5.2目盛りの位置 ―― (c)　　　　　　　　　　　　　
　よって(b)、(c)より  答　④