3-05-3: ガウスの法則の応用例：球電荷

球電荷はしばしば入試のテーマになります。しっかりマスターしましょう！

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

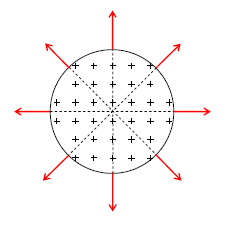
　図１のように、球体内に点電荷が一様に分布している（ある所は電荷が密集していたり、また別の所はまばらだったりすることがない）場合を「球対称電荷分布」と言い、略して「球電荷」と呼ぶことにする。各々の＋は点電荷\(q\)(>0)で、＋どうしの間隔は十分短く等しい（球なので奥行きもある）。まずはクーロンの法則の考え方で、球電荷のつくる電場\(\vec{E} \)がどのようになるのかを考察しよう。

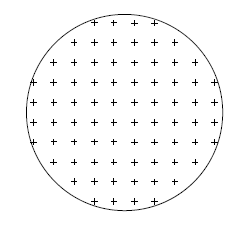
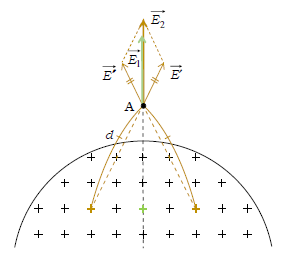
　図２の点Aは球外の１点で、点Aを通る半径方向(黒い点線)を上下方向に示してある。点Aの真下の＋(緑)が点Aにつくる電場\(\vec{E_1} \)(緑)は明らかに半径方向外向き。＋(緑)に関して左右対称の位置にある＋,+(黄)がつくる合成電場\(\vec{E_2}=\vec{E’}+\vec{E’’}\)(黄)も半径方向外向き、なぜなら、点Aから+,+(黄)までの距離がともに\(d\)だから\(\displaystyle E’=E’’=k\frac{q}{d^2} \)（3-02-1）で、平行四辺形の合成則が半径方向に関して左右対称な菱形の合成となるからである。このようにして、点Aの(全合成)電場\(\vec{E_A} \)は半径方向外向きであると分かる（図３）。　

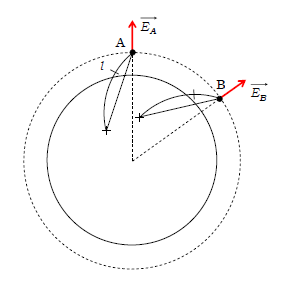
　今度は球の中心からの距離が点Aと等しい、別の点Bを考える（図３）。同様に、電場\(\vec{E_B} \)は半径方向外向きと分かる。[ ポイント下の第１段落で述べた「＋どうしの間隔は十分短く等しい」ことを思い出せば、点Bを通る半径方向について、図２の点Aと全く同様の状況がイメージできるだろう。] しかも、点Aから任意の＋までの距離を\(l\)とすれば、点Bから同じ距離\(l\)へだてた＋は必ず見つかる(図３)（図２の＋どうしの間隔は十分短いので）ことから、電場の強さ\(E_A=E_B \)である。結局、以下のような結論になる。

　ここまではクーロンの法則に基づいて考えてきたが、いざ電場の強さを計算するとなると、多数の電荷\(q\)のつくる電場を合成しなければならず、高校の範囲外である。そこで、これ以降はガウスの法則の考え方に切り替える。
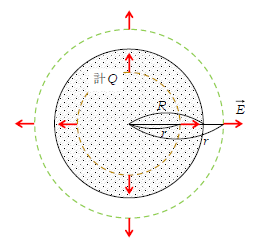
　図５では、半径\(R\)、電荷の合計\(Q\)の球電荷を、半径\(r\)（\(r≧R、r≦R\)）の球殻(点線)で覆ってある。球殻内部の電荷の合計を\(Q_{\text{in}}\)としよう。3-05-1と同様に、
　　閉曲面(球殻)を貫く力線の総数 \(=\) 1m\(^2\)あたり\(E\)本 × 力線が貫く表面積\(S\) (1)
　ここで表面積とは球殻の表面積だから\(S=4\pi r^2\)。3-05-1より(1)の左辺が\(\displaystyle 4\pi kQ_{\text{in}}\) と書けるから、
　　球電荷のつくる電場\(\displaystyle E=k\frac{Q_{\text{in}}}{r^2} \)　　　　　　　　　　　　　　　　　　　(2)

　ここからは場合分けで行こう。
１⃣　\(r≧R\)のとき（緑の点線）
　明らかに、球殻内部の電荷の合計\(Q_{\text{in}}=Q\)であるから、(2)より
　\(\displaystyle E=k\frac{Q}{r^2}\;\)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (3)
　これは、球の中心に点電荷\(Q\)があるとしたときの電場の公式と一致している。言い換えると、球電荷（広がりのある球対称電荷分布）はその外から見る場合、あたかも点電荷（点状）のように見てしまってかまわないということである。
２⃣　\(r≦R\)のとき（黄色の点線）
　ポイント下の冒頭で述べた通り、電荷の分布のしかたは一様であるから、図５より　
　\(Q_{\text{in}}:Q=\)球殻(点線)内部の体積 : 球の体積\(\displaystyle =\frac{4\pi}{3}r^3:\frac{4\pi}{3}R^3\)
　∴　\(\displaystyle Q_{\text{in}}=Q\frac{r^3}{R^3}\)　　(2)より
　\(\displaystyle E=k\frac{Q}{R^3} r\;\)　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (4)

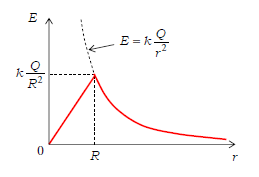
　(3)(4)をグラフにすると図６のようになる。球内部(\(r≦R\))では、\(r\)に比例して\(E\)も大きくなるところが興味深い。