5-10-1: 準静的断熱変化

式の導出過程が重要となる単元です。　→　＜続き＞は5-10-2へ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　単元タイトルの「準静的」 という語句は、5-06-1の通り「ピストンがほぼつり合いを保ちながらきわめてゆっくり動く」過程を指す。ならば、準静的でない方に含まれるのは、急激な状態変化。準静的でない断熱変化の代表例は「断熱混合」「断熱自由膨張」で、5-12-1のテーマにとしたい。この単元ではもっぱら準静的断熱変化を扱う。
　まずは断熱という条件を外し、かつ微小という条件を付加して、準静的微小変化で成り立つポイント(1)式を導こう。なお、ピストンのつり合いをほぼ保ちながら微小距離動かすことを何回も何回も繰り返すと、出だしで述べた準静的な変化が実現する。微小変化の繰り返しは準静的変化だ。ゆえに通常は準静的微小変化とは言わず、単に微小変化という。　　(＊)
　さて、今から記す(1)の導出過程は入試でよく出題されるのでしっかり行こう。
　初め圧力$P$、体積$V$、温度$T$の状態にある$n$[mol] の気体について、
　　状態方程式は$PV=nRT$（$R$: 気体定数）　　①
　この気体の圧力、体積、温度がそれぞれ微小量$\Delta P$、$\Delta V$、$\Delta T$変化した後では
　　$(P+\Delta P)(V+\Delta V)=nR(T+\Delta T)$　　②
　②÷①　$\displaystyle \left( 1+\frac{\Delta P}{P} \right) \left( 1+\frac{\Delta V}{V} \right) = 1+\frac{\Delta T}{T}$
　　∴　$\displaystyle 1+\frac{\Delta P}{P}+\frac{\Delta V}{V}+ \frac{\Delta P}{P}\frac{\Delta V}{V} = 1+\frac{\Delta T}{T}$
　2次の微小量$\displaystyle \frac{\Delta P}{P}\frac{\Delta V}{V}$ を無視すると（無視してよい 3-08-2）、
　$\displaystyle \frac{\Delta P}{P}+\frac{\Delta V}{V} = \frac{\Delta T}{T}$　　　　　　　　　　　　(1)
　この式は全ての微小変化について成り立つ。例えば定圧なら$\Delta P=0$より(1)は$\displaystyle \frac{\Delta V}{V} = \frac{\Delta T}{T}$となる。定積なら$\Delta V=0$より$\displaystyle \frac{\Delta P}{P} = \frac{\Delta T}{T}$ 。等温なら$\Delta T=0$より$\displaystyle \frac{\Delta P}{P}+\frac{\Delta V}{V} = 0$ 。断熱は$\Delta Q=0$であるが、式(1)の中に$\Delta Q$は入っていないので、(1)のまま用いる。

　次に、断熱の微小変化を扱う。微小変化は(＊)より準静的である。ポイント(2)式を導きたいのだが、今から記す(2)の導出過程もまた入試でよく出題されるのでしっかり行こう。
　熱力学第１法則$Q=\Delta U+W$の微小バージョン$\Delta Q=\Delta U+\Delta W$に、断熱の条件$\Delta Q=0$及び5-08-1の$\Delta U=nC_V\Delta T$（$C_V$は定積モル比熱）を代入すると
　$0=nC_V\Delta T+\Delta W$　　　　　　　　　　 　　③
　ここで微小仕事$\Delta W=P\Delta V$　　　　　　　　　④
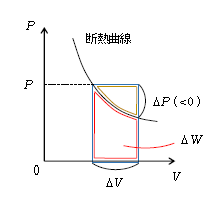
　さて、④は定圧の仕事$W=P\Delta V$という意味ではない。実は断熱変化は$P$-$V$グラフが図１のような右下がりの曲線(断熱曲線)になり（5-11-1で扱う）、$V$が増えると$P$は減っていく(定圧ではない)。ではなぜ④のように書けるのかというと ―― $P$が一定でない場合は、5-06-1の通り仕事$\Delta W=$$P$-$V$グラフの面積(図１の赤)。黄色は三角形に近いから、その面積を$\displaystyle \frac{1}{2}|\Delta P|\Delta V ×r$（rは例えば1.1のように選んだ適当な数）とでも書いてみる。すると、図１の青い長方形から黄色い部分の面積を引いて
　$\displaystyle \Delta W=P\Delta V-\frac{1}{2}|\Delta P|\Delta V ×r$
ところが、右辺第2項は$|\Delta P|\Delta V$の入っている2次の微小量だから無視すると（3-08-2）、$\Delta W=P\Delta V$となって④が言えるのである。
　同様の議論は、断熱変化に限らず$P$が一定でない全ての変化に当てはまる。つまり、仕事$W$ではなく微小仕事$\Delta W$を扱う限り、全ての状態変化で④が成り立つ。
　④を③に代入すると次式が得られる。
　$0=nC_V\Delta T+P\Delta V$　　　　　　　　　　　　(2)

　こうして得られた(1)、(2)を組合わせて式変形していくと、結論を先に言えば、(微小変化に限らず)準静的断熱変化で次が成り立つことが示せる。
　定圧モル比熱$C_P$と定積モル比熱$C_V$の比を比熱比$\displaystyle \gamma=\frac{C_P}{C_V}$として、
　　$PV^{\gamma}=$一定　　　　　　　　　　　　　　　　 (3)　　
これを「ポアソンの法則」という。
　ところで、「(1)、(2)を組合わせて式変形していく」中で実は積分計算をすることによって、$PV^{\gamma}=$一定が導かれることになる。この積分計算自体は大学入試で問われることはない。ただ、せっかくここまで説明したのだから、次の単元5-10-2で実際にこの積分計算を行って(PV^{\gamma}= \)一定を導く。興味のある人は見てほしい。
　(3)を用いると図１の$P$-$V$グラフが得られる、など準静的断熱変化のいろいろな説明や、さらには等温変化との対比は5-11-1に回す。