5-10-2: 準静的断熱変化(続き)
\(PV^{\gamma}= \)一定を導出します。数学で\(\displaystyle \lim_{\Delta x→0}\sum_{k=1}^{n} f(x_k) \Delta x = \int_a^b f(x)dx \)(区分求積法)を習った人向けです。
この単元では、5-10-1で導いた2つの式
\(\displaystyle \frac{\Delta P}{P}+\frac{\Delta V}{V} = \frac{\Delta T}{T} \, \) (1)
\(0=nC_V\Delta T+P\Delta V \, \) (2) を用いて
\(PV^{\gamma}= \)一定(ただし \(\displaystyle \gamma=\frac{C_P}{C_V} \)) (3) を証明する。
まず、(3)には\(T\)や\(\Delta T\)が含まれていないので、(1)、(2)中の\(T\),\(\Delta T\)を消去することから始めよう。具体的には(2)÷\(T\)とやって
\(\displaystyle 0=nC_V\frac{\Delta T}{T}+\frac{P}{T}\Delta V \) より\(\displaystyle \frac{\Delta T}{T}\)を求める。
\(\displaystyle \frac{\Delta T}{T}= -\frac{P}{nT}\frac{1}{C_V}\Delta V \)
状態方程式より得られる\(\displaystyle \frac{P}{nT}=\frac{R}{V} \) を代入して\(T\)を消去
\(\displaystyle \frac{\Delta T}{T}= -\frac{R}{V}\frac{1}{C_V}\Delta V=-\frac{R}{C_V}\frac{\Delta V}{V} \)
これを(1)に代入 \(\displaystyle \frac{\Delta P}{P}+\frac{\Delta V}{V} = -\frac{R}{C_V}\frac{\Delta V}{V}\)
これで\(T\),\(\Delta T\)は消去できた。次に\(\displaystyle \frac{\Delta V}{V} \)の項を右辺に移すと
\(\displaystyle \frac{\Delta P}{P} =-\left( 1+\frac{R}{C_V} \right) \frac{\Delta V}{V}= -\frac{C_V+R}{C_V}\frac{\Delta V}{V} \)
ここで5-09-1の\(C_P=C_V+R\)(マイヤーの関係式)を右辺の分子に代入すると
\(\displaystyle \frac{\Delta P}{P} = -\frac{C_P}{C_V}\frac{\Delta V}{V} \)
(3)のただし書きにあるように \(\displaystyle \gamma=\frac{C_P}{C_V} \) と表せば
\(\displaystyle \frac{\Delta P}{P} =-\gamma\frac{\Delta V}{V} \) (☆)
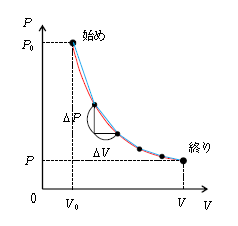
さて、図1を見てもらいたい。始めの状態から終りの状態にいたる\(P\)-\(V\)グラフの一例が赤い曲線で書かれている。これを微小かつ一定の横幅\(\Delta V\)の青い線分で区切る。最後には\(\Delta V →0\)の極限をとると、青い線分は赤い曲線に一致する。線分のタテは\(\Delta P\)、ヨコは\(\Delta V\)であるが、どの線分についても(☆)は成り立っている。そこで、図1の始めから終りにいたる全ての線分について(☆)の和をとると
\(\displaystyle \sum \frac{\Delta P}{P} =-\gamma\sum \frac{\Delta V}{V} \)
さらに\(\Delta V →0\)の極限をとると \(\displaystyle \lim_{\Delta P →0} \sum \frac{\Delta P}{P} =-\gamma \lim_{\Delta V →0} \sum \frac{\Delta V}{V} \)
区分求積法を用いれば \(\displaystyle \lim_{\Delta 〇→0} \sum \cdots \Delta 〇=\int \cdots d〇 \) のようになるから、
\(\displaystyle \int_{P_0}^{P} \frac{d P}{P} =- \gamma \int_{V_0}^{V} \frac{\Delta V}{V} \)
この定積分を行うと \(\displaystyle [\, \log_e P \,]_{P_0}^{P} =- \gamma [\, \log_e V \,]_{V_0}^{V} \)
以後、対数の底の\(e\)を省略すると \(\log P-\log P_0 =- \gamma (\log V-\log V_0) \)
∴ \(\log P+\log V^{\gamma}=\log P_0+\log V_0^{\gamma} \) ∴ \(\log PV^{\gamma}=\log P_0V_0^{\gamma} \)
よって \(PV^{\gamma}=P_0V_0^{\gamma}= \)定数 で(3)が証明された。


