6-10-1: 質量とエネルギーの等価性
\(E=mc^2\)は現代物理学の金字塔の式の1つです! → <例題>は6-10-2へ
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ \(E=mc^2\) \(E\): エネルギー、\(m\): 質量、\(c\): 光速=3.0×10\(^8\)m/s
・ 陽子、中性子、原子核\(\displaystyle ^{A}_{Z}\text{X} \)の質量をそれぞれ\(m_p\)、\(m_n\)、\(M\)とすると、
\(M c^2=Z m_p c^2+(A-Z) m_n c^2 – B \) \(B\): 結合エネルギー
\(B=\Delta m \cdot c^2 \) \(\Delta m\): 質量欠損
まずは核力について。これは核子どうしのあらゆるペアの間 ―― \(p\)-\(p\)間、\(n\)-\(n\)間、\(p\)-\(n\)間 ―― で働く極めて強力な引力である(図1)。そもそも原子核(大きさ10\(^{-15}\)m程度)というひじょうに狭い空間に閉じ込められた\(p\)-\(p\)どうしの間には、ひじょうに強いクーロン斥力が働く(クーロン力は距離の2乗に反比例(3-01-1)で距離が短いほど大きい)。この斥力をしのぐほどに強大な引力で、陽子\(p\)(及び中性子\(n\))を極微な空間に閉じ込めておくのが核力だ。核力の理論を1935年に提唱したのは、日本初のノーベル物理学賞を受賞した湯川秀樹博士である。参考までに、核子間の距離が10\(^{-15}\)mの数倍よりも長くなると核力は働かない。
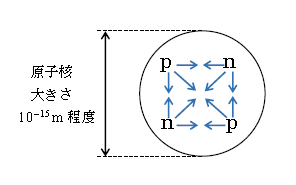
いま図1で、\(p,p,n,n\)どうしを互いに十分遠方へ引き離すことを考える。そのためには「核力に逆らって核子どうしをバラバラに引き離すための仕事」が必要で、「」の中身を結合エネルギーという。英語でbinding energyというので、頭文字を取って結合エネルギー\(B(^{4}\text{He}) \)のように表す(Heが原子番号2であることは周期表からすぐ分かることなので、左下の2は通常書かない)。
では、この単元のタイトルについて説明していく。質量とエネルギーの等価性を表す式\(E=mc^2\)は、1905年アインシュタインの発表した特殊相対性理論において提示され、今ではメディアでよく取り上げられるほど有名な式である。が、その広範な意味合いを理解するためには、特殊相対性理論及び一般相対性理論(ともに大学の課程)を習得しなければならない。ここでは大学入試にとって必要な、ごく狭い意味合いだけを述べる ――
核反応・放射性崩壊において、質量[\(\text{kg}\)]に\(c^2\)[m\(^2\)/s\(^2\)]をかけたものをエネルギー[\(\text{kg}\)・m\(^2\)/s\(^2\)=J] と見なした上でのエネルギー保存則が成り立つ。 (☆)
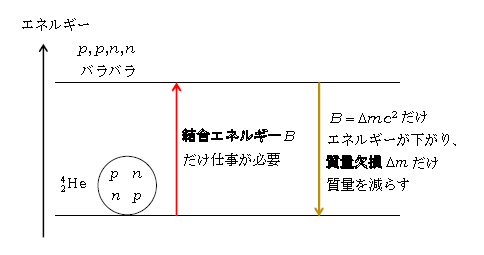
核反応 \(2p+2n →\;^{4}_{2}\text{He} \) を例に取ろう。右辺の原子核の状態\(^{4}_{2}\text{He} \) を、左辺の核子どうしバラバラな状態\(p,p,n,n\)に持っていくには、たった今述べた結合エネルギー\(B(^{4}\text{He}) \)が必要。よって、\(^{4}_{2}\text{He} \)よりも\(p,p,n,n\)の方がエネルギーの高い状態である(図2の赤い矢印)。逆に\(p,p,n,n\)から\(^{4}_{2}\text{He} \)に移るときは結合エネルギー\( B(^{4}\text{He}) \)だけエネルギーが低くなるので、その分のエネルギーが放出される。
(☆)を考慮してエネルギー保存則を書くと [ 陽子、中性子、\(^{4}_{2}\text{He} \)の質量は、通常それぞれ\(m_p\)、\(m_n\)、\(\displaystyle M(^{4}\text{He}) \)のように表す ]
\(2m_p c^2+2m_n c^2=M(^{4}\text{He}) c^2+B(^{4}\text{He}) \)
両辺を\(c^2\)で割ると
\(\displaystyle M(^{4}\text{He})=2m_p + 2m_n – \frac{B(^{4}\text{He})}{c^2} \)
つまり、\(^{4}_{2}\text{He} \)の質量は、その構成要素である核子どうしの質量の和\(2m_p+2m_n\)にはならず、それよりも\(\displaystyle \Delta m(^{4}\text{He})= \frac{B(^{4}\text{He})}{c^2} \)だけ低くなる。\(\Delta m\)を質量欠損という。質量欠損\(\displaystyle \Delta m=\frac{B}{c^2}\)は実験的に確かめられている厳然とした事実である。
質量とエネルギーの等価性(☆)の文脈で簡潔にまとめると、\(p,p,n,n\)から\(^{4}_{2}\text{He} \)へエネルギーが下がることと、質量が減ることとは等価である(図2の黄色い矢印)。
一般の原子核\(^{A}_{Z}\text{X} \)についても、図2と同様に原子核の方が核子のバラバラな状態よりもエネルギーが低い。よって、中性子数が\(A-Z\)(6-08-1)であることに注意して
\(M(^{A}\text{X}) \, c^2=Z m_p c^2+(A-Z) m_n c^2 – B(^{A}\text{X}) \)
\(B(^{A}\text{X})=\Delta m(^{A}\text{X}) \, c^2 \)
が成り立つ。
→ <例題>は6-10-2へ


