6-05-1: 電子波の干渉

電子の波動性の重要な例を解説します。　　　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　図１は結晶構造を持つ物質の表面を拡大したモデル図の例。図中の「格子面」とは、その面上で原子が規則正しく配列している面(左右方向の点線)である。上から順番に格子面1番、2番、3番、･･･と続く。左から入射してくるのは波動としての広がりを持つ「1個の」電子であることに注意してもらいたい。上から順番に電子1番、2番、3番、･･･がやって来るのではない。再度強調しておくが、あくまでも1個の電子が波動としての広がりを持ってやってくるのだ（6-04-1で述べた波動性と粒子性の二重性の1例である）。波動としての電子は格子面で入射角\(\theta\)=反射角\(\theta\)のように反射され、十分遠い観測点で干渉する（2-25-1の平行光線近似の作図を用いている）。なお、この単元では電子波の結晶表面での屈折は無視する。

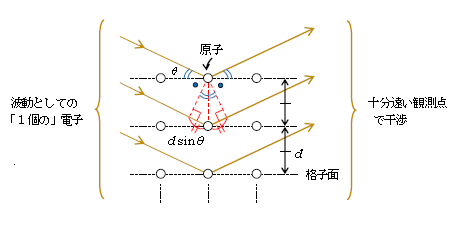
　反射波が強め合う条件を求めるために、格子面1番と2番で反射される電子波の経路差を調べよう。図１のように赤い点線の垂線を2本下したならば、\(\theta\)＋●＝90°であることから、図中の\(d\sin\theta\)の2倍分が経路差となる。つまり、格子面1番を通る反射波の経路より、2番の経路の方が\(2d\sin\theta\)だけ長い。
　この経路差が電子のドブロイ波長\(\displaystyle \lambda=\frac{h}{mv} \)(6-04-1)の整数倍に等しいと、格子面1番と2番の反射波が強め合い、以下同様に格子面2番と3番、3番と4番、･･･と全てが強め合って、観測点に強度の強い電子線が届く。よって
　反射波の強め合い： \(2d\sin\theta_n=n\lambda\)　(\(n=1,2,\cdots\))　　(☆)
　ここで電子が粒子性「だけ」を持つ小球のような存在だとしよう。すると、相手の原子の上側すれすれに当たるか中に寄った側に当たるかといった衝突のしかた次第で、入射角\(\theta\)に対して反射角は連続的な変数値を取るはずである。例えば入射角30°に対して反射角は20°…30°…40°…50°のような値を取れるだろう。しかし、(☆)を満たすような特定の入射角＝反射角\(\theta_n\)のみで強度が強くなるなら、それは電子が波動性を持つことの決定的証拠に他ならない。デイヴィソンとガーマーは(☆)のような結果を1927年ニッケルの単結晶の実験で実現させ、後にノーベル賞を受賞する。
　なお(☆)は、元々X線の回折及び干渉という別の現象で提示されていた式(1912年)であり、「ブラッグの法則」という。すなわち、図１で左から入射してくるのがX線(電磁「波」の一種)で、右の方で干渉する場合でも(☆)の式は成り立つ。