5-13-1: 熱サイクル <例題>
熱力学の総仕上げに入ります! → 関連事項は5-13-2へ
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
例題
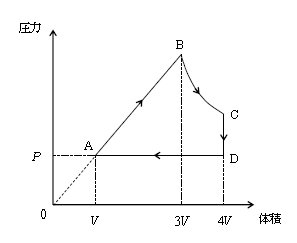
なめらかに動くピストンの付いたシリンダーに一定の物質量の単原子分子理想気体を封じ込め、図のように状態A→B→C→D→Aの順序で変化させる1サイクルを考える。A→Bは圧力と体積の比が一定の状態変化、B→Cは断熱変化、C→Dは定積変化、D→Aは定圧変化である。状態Aでの圧力を\(P\)、体積を\(V\)とし、気体定数を\(R\)とする。なお、断熱変化では(圧力)×(体積)\(\displaystyle^{\frac{5}{3}} =\)一定であることを用いてよい。
問1 状態A→Bで気体が外部にする仕事\(W_1\)及び気体が吸収する熱量\(Q_1\)を求めよ。
問2 状態Bでの温度はAでの温度の何倍か。
問3 状態Cでの温度はAでの温度の\(\alpha\)倍であるとする。\(\alpha=\) (\(\cdots\))\(\displaystyle ^{\frac{4}{3}} \)の形に表せ。
以下では\(\alpha\)を答に用いてよい。
問4 状態B→Cで気体が外部にする仕事\(W_2\)を求めよ。
問5 この1サイクルで気体が外部にする仕事の合計\(W’\)を求めよ。
問6 この1サイクル中の吸熱過程において、気体が吸収した熱量の合計\(Q’\)を求めよ。
解答・解説
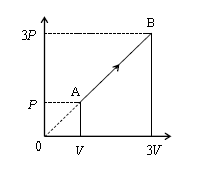
問1 5-06-1の仕事\(W=P\)-\(V\)グラフの面積を用いる。問題文中に「A→Bは圧力と体積の比が一定」とあるから、A→Bで横軸が\(V\)から\(3V\)の3倍になると、縦軸も3倍になる。ゆえにBの圧力\(P_B=3P\) 。
\(W_1=\)図1の台形の面積\(=(P+3P)×(3V-V)÷2=\) 答 \(4PV \)
次に熱力学第1法則\(Q=\Delta U+W\)を用いる。単原子分子気体の\(U=\frac{3}{2}nRT=\frac{3}{2}PV \)(5-04-3)より、
内部エネルギー変化\(\Delta U_1=\)あとの\(\displaystyle \frac{3}{2}PV\) \(-\) まえの\(\displaystyle \frac{3}{2}PV\)
\(\displaystyle =\frac{3}{2}(P_BV_B-P_AV_A)=\frac{3}{2}(3P3V-PV)=12PV \)
∴ \(\displaystyle Q_1=\Delta U_1+W_1=12PV+4PV=\) 答 \(16PV \)
問2 モル数\(n\)として、状態方程式A: \(PV=nRT_A\) (1)
B: \(3P3V=nRT_B\)
下の式÷上の式を右辺から書いて \(\displaystyle \frac{T_B}{T_A}=\) 答 \(9 \)
問3 問題文中に「断熱変化では\(\displaystyle PV^{\gamma} =\)一定(ただし単原子分子の場合\(\displaystyle \gamma=\frac{5}{3} \)) とあるのは、5-11-1で説明した通り。いま温度\(T_C\)を求めたいから、5-11-1の\(TV^{\gamma-1} = \)\(\displaystyle TV^{\frac{2}{3}}= \)一定 を用いることにしよう。
∴ \(\displaystyle T_CV_C^{\frac{2}{3}} =T_B V_B^{\frac{2}{3}} \)
問2より\(T_B=9T_A\)だから \(\displaystyle T_C(4V)^{\frac{2}{3}} =9T_A(3V)^{\frac{2}{3}} \)
\(\displaystyle V^{\frac{2}{3}} \)を約して \(\displaystyle \frac{T_C}{T_A}=9\left( \frac{3}{4}\right)^{\frac{2}{3}} \)
ここで \(\displaystyle 9=3^2=(27^{\frac{1}{3}})^2=27^{\frac{2}{3}}\) だから
\(\displaystyle \alpha=\frac{T_C}{T_A}=27^{\frac{2}{3}}\left( \frac{3}{4}\right)^{\frac{2}{3}}=\left( \frac{81}{4}\right)^{\frac{2}{3}}= \left( \left( \frac{9}{2}\right)^2 \right)^{\frac{2}{3}}=\) 答 \(\displaystyle \left( \frac{9}{2}\right)^{\frac{4}{3}} \)
問4 断熱変化B→Cの\(W=P\)-\(V\)グラフの面積 で計算しようとすると、問題の図中にあるようなB→Cの曲線の面積を求めなければいけない。理屈の上では面積は積分計算で求めることはできるが、いかにも大変。もっとマシな方法を用いる。
断熱では熱力学第1法則より\(Q=0=\Delta U+W\)なので、\(W=-\Delta U\)と行くのがよい。
\(\displaystyle W_2=-\Delta U_2=-\left( \frac{3}{2}nRT_C-\frac{3}{2}nRT_B \right) \)
問2より\(T_B=9T_A\) 、問3より\(T_C=\alpha T_A\) だから
\(\displaystyle W_2=\frac{3}{2}nR(9T_A-\alpha T_A)=\frac{3}{2}(9-\alpha)nRT_A \)
\(n,T_A\)は自分でおいた(問題文中にない)文字だから答に使えない。(1)を用いて
\(\displaystyle W_2=\) 答 \(\displaystyle \frac{3}{2}(9-\alpha)PV \)
問5 定積変化C→Dの仕事\(W_3=0\)
定圧変化D→Aの仕事\(W_4=P\Delta V=P(V_A-V_D)=P(V-4V)=-3PV\)
問1の\(W_1\) 、問4の\(W_2\)を用いて
合計\(\displaystyle W’=W_1+W_2+W_4=4PV+\frac{3}{2}(9-\alpha)PV-3PV\)
\(=\) 答 \(\displaystyle \frac{1}{2}(29-3\alpha)PV \)
問6 A→Bは問1より吸熱\(Q_1=16PV \)
B→Cは断熱\(Q_2=0 \)
定積C→Dは\(Q_3=nC_V\Delta T \)と書ける(5-08-1の(1)式を参照)。\(PV=nRT\)で\(V\)一定で、C→Dで\(P\)が下がるから、\(T\)も下がる。ということは\(\Delta T<0\)なので\(Q_3<0\)すなわち放熱である。ゆえに\(Q_3\)は問題文中の「吸熱過程」には含めない。
定圧D→Aは\(Q_4=nC_P\Delta T \)と書ける。\(PV=nRT\)で\(P\)一定で、D→Aで\(V\)が減るから、\(T\)は下がる。ということは\(\Delta T<0\)なので\(Q_4<0\)これも放熱。ゆえに\(Q_4\)も吸熱過程には含めない。
以上から、吸熱の合計\(Q’=Q_1=\) 答 \(16PV \)


