5-13-2: 熱効率
熱効率の2つの表現をしっかり押さえましょう!
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ 熱効率
\(\displaystyle e=\frac{W_{tot}}{Q_+}\) と定義する。
\(W_{tot}\): 外部にした仕事の合計 、\(Q_+\): 吸熱過程で吸収した熱量の合計
\(\displaystyle e=1-\frac{|Q_-|}{Q_+} \) とも書ける(|\(Q_-\)|: 放熱過程で放熱した熱量の合計)
・ \(W_{tot}=\; \pm\) (\(P\)-\(V\)図で囲まれた面積) (右回りサイクルは\(+\)、左回りは\(-\))
初めに用語の説明として、熱機関(heat engine)とは、熱量の一部を仕事に変換する装置をいう。engineという言葉から分かる通り、自動車や飛行機のエンジンがその代表例。熱機関はしばしば理想気体の\(P\)-\(V\)サイクル(\(P\)-\(V\)図上で1周して元に戻るような過程、図1)としてモデル化される。ただし、5-12-1で述べた通り急激な状態変化は\(P\)-\(V\)グラフに表すことができない。理論的にはゆっくりとした(準静的な)変化のみが\(P\)-\(V\)グラフに書ける。しかし現実のエンジンはもちろん高速回転させたりなど急激な変化はザラだから、それを\(P\)-\(V\)図として表すのは、あくまでモデル(単純化・理想化した理論的設定)としてのことである。
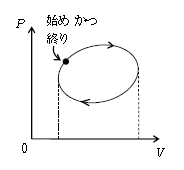
今度は、\(P\)-\(V\)サイクル(熱機関のモデル)の熱効率\(e\)という用語の説明。まず、サイクル1周で気体が外部にした仕事の合計を\(W_{tot}\)(添え字はtotalの略)とする。これは正の仕事をする過程、負の仕事の過程ひっくるめた合計という意味で、よく「正味の仕事」という言い方をする。次に、サイクル1周における吸熱過程で気体が吸収した熱量の合計を\(Q_+\)とする。これには放熱過程での熱量の合計\(Q_-\) (\(<0\)) を含めない。すると、定義により
熱効率 \(\displaystyle e=\frac{W_{tot}}{Q_+}\) (1)
分母の\(Q_+\)には気体の受け取るエネルギーという意味があり、分子の\(W_{tot}\)には受け取ったエネルギーの一部を外部への仕事として変換し有効利用する分という意味がある。したがって効率\(e\)とは「受取り分の有効利用の割合」のことである。ところで、放熱\(|Q_-|\) (\(Q_-<0\)) にはムダに捨てるエネルギーという意味がある(放熱は環境用語としてしばしば排熱と呼ばれる)。よって「受取り分の有効利用の割合」\(e\)の分母には\(Q_-<0\)を含めないのだ。
効率\(e\)の式を書き換えてみよう。それには1サイクルでの熱力学第1法則
\(Q_{tot}=\Delta U_{tot}+W_{tot}\) (2) を用いる。
まず、\(Q_{tot}=Q_+ +Q_-=Q_+ -|Q_-|\) [ \(Q_-<0\)だから、たとえば\(Q_-=-50\) J 。それで \(Q_+ +Q_-=Q_- -50\) J \(=Q_+ -|Q_-|\) となる ]
次に\(\Delta U_{tot}=nC_V\Delta T_{tot}\) であるが、1サイクルでは1周して元に戻るから(図1)、サイクル始めの温度とサイクル終り(始めに戻っている)の温度は当然等しい(\(T_{始}=\frac{1}{nR} P_{始}V_{始}=\frac{1}{nR} P_{終}V_{終}=T_{終}\))。ゆえに\(\Delta T_{tot}=0\) で\(\Delta U_{tot}=0\) 。
すると(2)より \(W_{tot}=Q_+ -|Q_-| \: \) (3)
この式には、「吸熱\(Q_+\)のうち、放熱\(|Q_-|\)以外は、\(W_{tot}\)として有効利用される」という分かりやすい意味がある。(3)を(1)に代入すると
熱効率\(e=\)\(\displaystyle \frac{Q_+ -|Q_-|}{Q_+}=\)\(\displaystyle 1-\frac{|Q_-|}{Q_+} \) (1′)
入試で効率\(e\)を求めるときは、(1)と(1′)のどちらが有利になるかあらかじめ見通しを立てておくのが大切である。たとえば5-13-1の例題では、問5で\(\displaystyle W_{tot}=W’=\frac{1}{2}(29-3\alpha)PV \)が求まり、問6で\(Q_+=Q’=16PV \) が求まっているから、(1)を用いて
\(\displaystyle e=\frac{W’}{Q’} =\frac{1}{32}(29-3\alpha)\) とするのがよい。 [ 参考までに、問3で\(\displaystyle \alpha=\left( \frac{9}{2}\right)^{\frac{4}{3}} \) だったが、電卓で計算すると\(\alpha=\)7.429… 、これを代入して \(e=\)0.210=21% である。 ]
一方、たとえば\(Q_+\)、\(|Q_-|\)がすでに求まっていて\(W_{tot}\)が未知のような場合はもちろん(1′)を用いる。
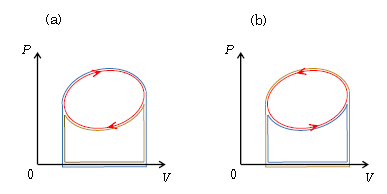
最後に \(W_{tot}=\; \pm\) (\(P\)-\(V\)図で囲まれた面積) (☆)
の説明をしておく(図2)。図2(a)、(b)はそれぞれ右回り、左回りのサイクルである。まず(a)で、正の仕事\(W_+\)をする膨張過程の面積が青い部分、負の仕事\(W_-\)をする圧縮過程の面積が黄色、ゆえに\(W_{tot}\)\(=W_+ +W_-\)\(=W_+ -|W_-|\)は青から黄色を引いた赤い部分の面積になり(☆)が言える。一方(b)では、\(W_+\)の青い面積よりも\(W_-\)の黄色の面積の方が大きい。ゆえに\(W_{tot}=W_+ -|W_-|<0\)となるから、 \(W_{tot}=\; -\) (\(P\)-\(V\)図で囲まれた面積) として(☆)が言える。 [ なお、\(W_{tot}<0\)ということは上に述べた有効利用をできないことを意味する。ゆえに左回りサイクルは熱機関としては役に立たず、別の用途に用いられるが、ここでは深入りしない。]