3-12-2:誘電体を入れたコンデンサーの容量
この単元の数式を手書きしながら読破すれば、かなり力が付きます!
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
以下、パターン1,2について合成容量を求めていく。この単元に限り、ポイントは説明文途中にまとめる。
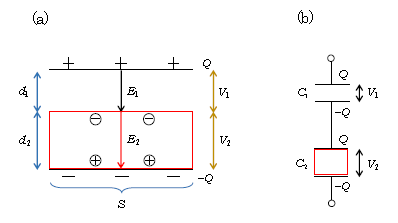
□ パターン1 図1(a)の状況を考える(赤色が誘電体)。3-08-1のコンデンサーの3大公式に基づいて考えていく。
まずは真空部分から
第1公式:電荷から電場ができる。真空中の電場\(\displaystyle E_1=\frac{Q}{\epsilon_0 S} \)
第2公式:電場に沿って電位が下がる。電位差\(\displaystyle V_1=E_1 d_1=\frac{Q}{\epsilon_0 S} d_1=\frac{d_1}{\epsilon_0 S} Q \)
第3公式 : \(Q\)は\(V_1\)に比例。\(Q=C_1 V_1\)と書ける。
∴ \(\displaystyle C_1=\frac{Q}{V_1}=\frac{\epsilon_0 S}{d_1}\)
\(C_1\)の式の形から、真空部分は面積\(S\)、間隔\(d_1\)の真空コンデンサーと見なせることが分かる。 (1)
次に誘電体部分
第1:誘電体中の電場は3-11-1の通り \(\displaystyle E_2=\frac{1}{\epsilon_r} E_1\) 上の\(E_1\)を代入して \(\displaystyle E_2=\frac{1}{\epsilon_r}\frac{Q}{\epsilon_0 S} \)
第2:\(\displaystyle V_2=E_2 d_2=\frac{1}{\epsilon_r} \frac{Q}{\epsilon_0 S} d_2=\frac{1}{\epsilon_r} \frac{d_2}{\epsilon_0 S} Q \)
\(\displaystyle \)第3:\(Q=C_2 V_2\)と書ける。\(\displaystyle C_2=\frac{Q}{V_2}=\epsilon_r\frac{\epsilon_0 S}{d_2}\)
面積\(S\)、間隔\(d_2\)の真空コンデンサーの容量を\(C_0\)とでもおくと、\(C_2=\epsilon_r C_0\) 。この数式は、3-12-1でやった通り、コンデンサーの極板間を誘電体ですき間なく満たすと容量が\(\epsilon_r \)倍になる式を思い出させる。
ということは、\(C_2\)の式の形から、誘電体部分は誘電体をすき間なく満たした面積\(S\)、間隔\(d_2\)のコンデンサーと見なせることが分かる。 (2)
合成容量の定義は3-10-1より \(\displaystyle C=\frac{端子に流れ込む電荷}{端子間電圧}=\frac{Q}{V_1 +V_2} \)
逆数にすれば \(\displaystyle \frac{1}{C}=\frac{V_1}{Q}+\frac{V_2}{Q}=\frac{1}{C_1}+\frac{1}{C_2} \) これは直列合成公式に他ならない。
ポイント1 図1(a)のような配置を見たら、まず直観的に図1(b)の配置となることを見通す。次に(1)にならって\(\displaystyle C_1=\frac{\epsilon_0 S}{d_1}\)とし、(2)にならって\(\displaystyle C_2=\)\(\epsilon_r\)×\(\displaystyle \frac{\epsilon_0 S}{d_2}\)とする。最後に直列合成公式を使えばよい。
従って \(\displaystyle \frac{1}{C}=\frac{d_1}{\epsilon_0 S}+\frac{1}{\epsilon_r}\frac{d_2}{\epsilon_0 S}=\frac{1}{\epsilon_0 S} \left(d_1+\frac{1}{\epsilon_r}d_2 \right)=\frac{1}{\epsilon_0 S} \frac{\epsilon_r d_1+d_2}{\epsilon_r} \)
∴ \(\displaystyle C=\frac{\epsilon_r \epsilon_0 S}{\epsilon_r d_1+d_2} \)
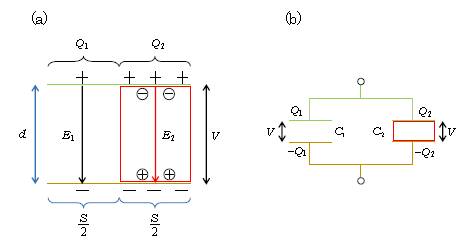
□ パターン2 図2(a)の状況を考える(赤色が誘電体)。
まずは真空部分
第1公式:\(\displaystyle E_1=\frac{Q_1}{\epsilon_0 \frac{S}{2}} \)
第2公式:\(\displaystyle V=E_1 d=\frac{Q_1}{\epsilon_0 \frac{S}{2}} d=\frac{d}{\epsilon_0 \frac{S}{2}} Q_1 \)
第3公式 : \(Q_1\)は\(V\)に比例。\(Q_1=C_1 V\)と書ける。
∴ \(\displaystyle C_1=\frac{Q_1}{V}=\frac{\epsilon_0 \frac{S}{2}}{d}\)
\(C_1\)の式の形から、真空部分は面積\(\displaystyle \frac{S}{2}\)、間隔\(d\)の真空コンデンサーと見なせることが分かる。 (3)
次に誘電体部分
第1:誘電体部分をいったん真空に見立てると、真空中の電場\(\displaystyle E_0=\frac{Q_2}{\epsilon_0 \frac{S}{2}} \) 。実際には誘電体中の電場は弱まるから、\(\displaystyle E_2=\frac{1}{\epsilon_r} E_0\) 。\(E_0\)を代入して \(\displaystyle E_2=\frac{1}{\epsilon_r} \frac{Q_2}{\epsilon_0 \frac{S}{2}} \) (4)
第2:\(\displaystyle V=E_2 d=\frac{1}{\epsilon_r} \frac{Q_2}{\epsilon_0 \frac{S}{2}} d=\frac{1}{\epsilon_r} \frac{d}{\epsilon_0 \frac{S}{2}} Q_2 \)
第3:\(Q_2=C_2 V\)と書ける。\(\displaystyle C_2=\frac{Q_2}{V}=\epsilon_r\frac{\epsilon_0 \frac{S}{2}}{d}\)
\(C_2\)の式の形から、誘電体部分は、誘電体をすき間なく満たした面積\(\displaystyle \frac{S}{2}\)、間隔\(d\)のコンデンサーと見なせることが分かる。 (5)
合成容量 \(\displaystyle C=\frac{端子に流れ込む電荷}{端子間電圧}=\frac{Q_1 +Q_2}{V}=C_1 +C_2 \) これは並列合成公式に他ならない。
ポイント2 図2(a)のような配置を見たら、まず直観的に図2(b)の配置となることを見通す。次に(3)にならって\(\displaystyle C_1=\frac{\epsilon_0 \frac{S}{2}}{d}\)とし、(5)にならって\(C_2=\)\(\epsilon_r\)×\(\displaystyle \frac{\epsilon_0 \frac{S}{2}}{d}\)とする。最後に並列合成公式を使う。
よって \(\displaystyle C=\frac{\epsilon_0 \frac{S}{2}}{d}+\epsilon_r \frac{\epsilon_0 \frac{S}{2}}{d}= \frac{1+\epsilon_r}{2}\frac{\epsilon_0 S}{d} \)
ところで、図2(a)の上極板全体がひとつながりの導体だから等電位という意味で緑色を施してある。同様に下極板全体も等電位(黄色)。誘電体側の緑と黄色の電位差が\(V\)であるのみならず、真空側も緑と黄色の差なので\(V\)。すると、第2公式\(V=E_1 d=E_2 d\)より、\(E_1=E_2\)と分かる。待てよ、誘電体は電場を弱める性質があるはずなのに、\(E_1=E_2\)とはどういうことだ?その理屈は ―― 結論を先に述べるなら、図2(a)に示した通り、真空側よりも誘電体側の方がコンデンサーの極板の電荷が多いのだ(例えば真空側は+が1個に対して誘電体側は+が3個)。すなわち\(Q_1<Q_2\)なので、電場\(\displaystyle \frac{Q_1}{\epsilon_0 \frac{S}{2}}<\frac{Q_2}{\epsilon_0 \frac{S}{2}}\)。この左辺が図2(a)の\(E_1\)で、右辺を\(\frac{1}{\epsilon_r}\)倍に弱めたものが\(E_2\)((4)式)で、結局\(E_1=E_2\)になっているのである。
このように、誘電体側の方が真空側よりも電荷を多く「誘」い込むのだ。


