3-10-1: 合成容量

合成容量の定義式をしっかり押さえることが、後々の応用問題で重要になってきます！　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　2個のコンデンサーについて理解できれば、\(n\)個への一般化は容易だ。2個の場合の説明をしよう。
　並列接続とは、図1(a)のようにコンデンサー（横２本線がその回路記号）を横並びにして導線でつないだもの。その特徴として、2つのコンデンサーの電圧\(V\)がともに等しい。というのも、緑色を施した部分は導線と2つのコンデンサーの上側の極板から成り、全体がひとつながりの導体をなしている（導線も極板も金属である）。3-06-1でやった通り、(帯電完了後)ひとつながりの導体は等電位だから、緑全体が等電位。同様に青全体も等電位。コンデンサーの電圧(電位差)とは、正極板から負極板への電位の下がり分のことで、今の場合左右のコンデンサーともに緑から青への下がり分となって電圧が等しいというわけである。並列接続は電圧が共通だ。
　このとき、3-08-1の通り、電荷\(Q_1=C_1 V\)、\(Q_2=C_2 V\)　　(1)

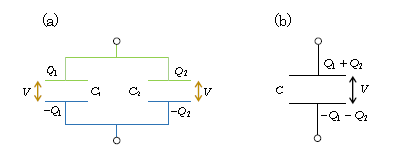
　ところで上端と下端に付けた丸印は「端子」を表す記号で、この場合は上端が＋の端子、下端がーの端子。それぞれ電池の正極、負極につながれている（またはつながれていた）ことが想定されている（図2）。図1(a)と(b)を比べると、ともに同じ端子間電圧\(V\)の下、等しく\(Q_1+Q_2\)の電荷をたくわえているという意味で、(a)と(b)は等価(回路)であるという。例えば＋とーの端子間をブラックボックスの中に入れてしまうと、外目にはどちらが(a)でどちらが(b)か言い当てることはできないだろう（もちろん、例えば重さを測定すれば区別は付くだろうが。ブラックボックスはあくまでイメージのお話）。この等価回路の容量を並列合成容量という。すなわち
　合成容量 \(C=\)\(\displaystyle \frac{端子に流れ込む電荷}{端子間電圧}\)\(\displaystyle =\frac{Q_1+Q_2}{V} \)　と定義する。
　\(\displaystyle\)すると、\(\displaystyle C=\frac{Q_1}{V}+\frac{Q_2}{V} \)　(1)式を用いて \(C=C_1+C_2\) となる。

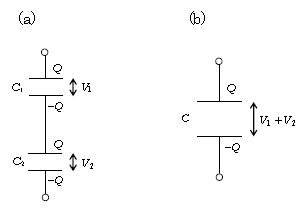
　次なる話は直列接続（図3(a)）、すなわちコンデンサーを数珠(じゅず)つなぎつなぎにしたもの。2つのコンデンサーの電荷を\(Q_1,Q_2\)のようにはせずに、ともに\(Q\)とした理由は後ほど。
　このとき、\(Q=C_1 V_1\)、\(Q=C_2 V_2\)　　(2)
　さて、図3(a)と(b)は、ともに同じ端子間電圧\(V_1+V_2\)の下、等しく\(Q\)の電荷をたくわえているという意味で等価である。よって、
　合成容量 \(\displaystyle C=\frac{端子に流れ込む電荷}{端子間電圧}\)\(\displaystyle =\frac{Q}{V_1+V_2}\)　
　あるいは逆数をとると、\(\displaystyle \frac{1}{C}=\frac{V_1}{Q}+\frac{V_2}{Q}\)
(2)式を用いて \(\displaystyle \frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2} \)　となる。
　ここで、2つのコンデンサーの電荷がともに\(Q\)ではなく、\(Q_1,Q_2\)のように異なると、今の議論は成り立たない。よって、直列合成容量の公式は2つのコンデンサーの電荷が共通の場合のみ成立する。重要な点だからしっかり銘記しておこう。