2-19-2: レンズの公式 ＜例題＞

例題を通じてレンズの理解を深めましょう！　　　　　　　　　　　　　　　　　　　　　　　　　　　　

例題　

　凸レンズのはたらきについて考えよう。図１のように、レンズから距離$a$の位置に物体を置いたとき、レンズから距離$b$の位置に像ができた。図２は$a$と$b$の関係を表すグラフである。ただし、$b$が負の値をとるのは、レンズから見て物体側に像ができるときである。

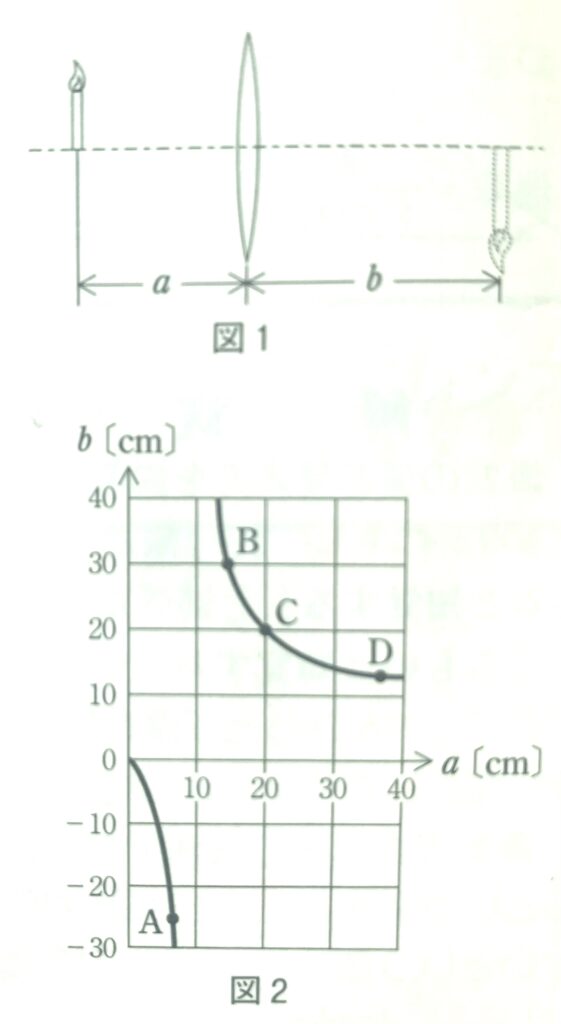
問１　このレンズの焦点距離はいくらか。最も適当な数値を、次の①～④のうちから一つ選べ。
①　5　②　10　③　20　④　40
問２　像と物体の位置が、図２中の点Bで与えられるとき、像の大きさは物体の大きさの何倍か。最も適当な数値を、次の①～⑤のうちから一つ選べ。
①　$\displaystyle \frac{1}{3}$　②　$\displaystyle \frac{1}{2}$　③　1　④　2　⑤　3
問３　このレンズを虫めがねとして用いるためには、図２中のA～Dのどこで使えばよいか。最も適当なものを、次の①～④のうちから１つ選べ。
①　A　②　B　③　C　④　D　
問４　レンズの下半分を黒い紙で覆った。このとき、像はどのように変化したか。最も適当なものを、次の①～⑥のうちから一つ選べ。
①　像の下半分が見えなくなった。　　
②　像の上半分が見えなくなった。　
③　像全体が暗くなった。　
④　像全体が明るくなった。　
⑤　像が小さくなった。　
⑥　像が大きくなった。

解答・解説

(＊)　問題文「$b$が負の値をとるのは、レンズから見て物体側に像ができる」とは、2-19-1図２の虚像ができる場合。
　2-19-1図２ではレンズの公式は　$\displaystyle \frac{1}{a} +\frac{1}{-b} =\frac{1}{f}$　だったが、この問題では、$-b$の代わりに$b$($<0$)を用いて　$\displaystyle \frac{1}{a} +\frac{1}{b} =\frac{1}{f}$　　つまり$b$に符号を含めている。混乱しないように。

問１　図２の点Cで$a$＝cm、$b$＝cmを読み取れば、レンズの公式
　$\displaystyle \frac{1}{a} +\frac{1}{b} =\frac{1}{f}$（2-19-1図２の場合）が使える。
　$\displaystyle \frac{1}{20\text{cm}} +\frac{1}{20\text{cm}} =\frac{1}{f}$　　∴　$f$=10cm　
　答　②
問２　図２の点Bでは$a$=15cm、$b$＝30cmだから、
　倍率$\displaystyle =\frac{b}{a} =\frac{30\text{cm}}{15\text{cm}} =2$　　　　答　④
問３　虫めがねとは、2-19-1図２のように物体を凸レンズと焦点の間に置く場合だ。するとレンズの前方に、正立虚像が必ず拡大されて見える（2-19-1図３の凹レンズでは、正立虚像が縮小されてしまうから、虫めがねとして使えない）。(＊)の下線部より、$b<0$となるものを図２のグラフから選べばよいから、答は点A　　　　
　答　①
問４　2-19-1図aの後の段落で、「様々な光全てがレンズの後方の１点で交わる」と説明があったのを思い出そう。するとレンズの下半分を覆っても、下図のように矢印の先端(青丸)から足元(黄色丸)まで像は結ばれることが分かる。像の上半分や下半分が欠けることはない。ただしレンズの下半分の光(点線)が届かないから、光量は減って像は暗くなる。　　　　
　答　③