10-01-1: 運動の第1法則「F=0ならa=0」は第2法則ma=Fに含まれる？

物理を習ったことのある人なら誰もが抱く疑問を明快に解き明かします！ 中級者向きの内容です。　→　＜続き＞は10-01-2へ　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　物理を習ってしばらくすると（あるいは目ざとい人はすぐに）気付くだろうことがある。それは ――
　運動の第１法則（慣性の法則）「物体に力が働かないと、物体は等速直線運動を続け、特に初め静止していたなら静止し続ける」
　運動の第２法則（運動方程式）「\(m\vec{a}=\vec{F} \)」
に関してのこと。第２法則の右辺で\(\vec{F}=0 \)とすると、左辺の\(\vec{a}=0 \)が得られるから、「物体に力が働かないと\(\vec{F}=0 \)、物体は加速しない\(\vec{a}=0 \)、つまり等速のまま」であることが導けた、これを慣性の法則(第１法則)という、めでたし、めでたし…。
　しかし、ここで少し考えてみると気付くのだが、今言ったことは第２法則を使って第１法則を証明したということ。第２から簡単に証明できてしまうような法則（物体に力が働かないと、物体は等速）を、わざわざ第１法則として打ち立てる必要はあるのだろうか

慣性系と非慣性系

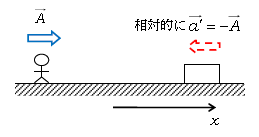
　ここで、簡単な考察（思考実験）をしてみよう。大地に対して加速度\(\vec{A} \)で右向きに運動する観測者が、大地に対して静止している物体を眺めているとする（図１）（物体側ではなく、観測者側の加速度という意味合いを込めて、あえて大文字の\(\vec{A} \)を用いている）。するとこの物体は、左向きの加速度\(-\vec{A} \)で相対的に観測者に近づいてくるように見える。観測者と物体の間の距離はどんどん詰まっているからだ。これを称して物体の相対加速度\(\vec{a’} =- \vec{A} \)であるという。一方、この静止している物体には当然何も力は加わっていない。仮に力が加われば物体は静止できずに動き出してしまう。ゆえにこの物体の運動方程式\(m\vec{a}=\vec{F} \)は
　　\(m\vec{a’} =\vec{F}=\vec{0}\)　つまり \(m(-\vec{A}) =\vec{0} \)　ゆえに左辺\(\ne \vec{0} \)、右辺\( =\vec{0} \)　　(＊)
となって、明らかに矛盾である。

　この矛盾を解決するために導入されるのが「慣性力」だ。慣性力とは、「加速度\(\vec{A} \)で運動する観測者は、通常の力（重力、垂直抗力、張力、…）以外に、見かけ上の力\( (-m\vec{A}) \)を観測する」というときの\( (-m\vec{A}) \)のこと。例えば加速度\(\vec{A} \)で急発進する電車の乗客は、つり革が電車の進行方向と逆向きに傾くのを観測するが、あれも慣性力\( (-m\vec{A}) \)のなせる業である。というのも、\( (-m\vec{A}) \)とマイナスの符号が付いていることから、観測者(乗客)の加速度=乗っている電車の加速度\(\vec{A} \)(進行方向)　と逆向きに働いて、つり革を逆向きに傾かせるというわけだ。
　慣性力という用語のニュアンスはこうだ ―― つり革には本来なら力が働いていないから、慣性の法則(力が働かないと、物体は等速、特に初め静止していれば静止し続ける)によって、その場にとどまっていようとするはずである。言いかえると、電車が急発進したのに対して、進行方向逆向きにつり革を引き留めておこうとするような慣性の法則的な効果が生じている。それで慣性力という名が付いている。

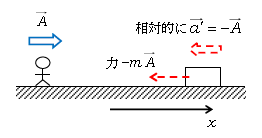
　図１に新たに慣性力を加えたのが図２。すると物体の運動方程式\(m\vec{a}=\vec{F} \)は
　　\(m\vec{a’} =\vec{F}=-m\vec{A} \)　つまり \(m(-\vec{A}) =-m\vec{A} \)
となって、左辺＝右辺の等号が成立、(＊)の矛盾は慣性力\( (-m\vec{A}) \)によって無事解決されている。
　なお、慣性力\( (-m\vec{A}) \)は(＊)のいわば「数式上の」矛盾を解消するために導入された見かけ上の力だから、「何から」働く力ということが言えない。これが通常の力、例えば重力であれば「地球から」働く、張力であれば「糸から」働くと言えるのと大違いな点。慣性力については、「AからBに」働く力といったことが言えないので、その反作用「BからAに」働く力も存在しない。つまり慣性力は運動の第３法則（作用反作用の法則）を満たさない。

　さて、物理では「観測者」という用語と「座標系」という用語をほぼ同義語として用いる。大地に静止した「観測者」が現象を記述することと、大地に静止した「座標系」(\(x\)軸や\(y\)軸など)を設定して現象を記述することとは同じ意味。大地に対して「加速度運動する観測者」と言えば、その人自身に固く結びついた「加速度座標系」（座標系自体が大地に対して加速度運動している）を想定しているという意味。
　すると、この思考実験（図１）から次のことも言える ――
　加速度座標系においては慣性の法則(物体に力が働かないと、物体は等速)が成り立たない。なぜなら、図１では力が働いていないにもかかわらず、物体には(相対)加速度\(\vec{a’} =- \vec{A} \)が生じている。
　これに比して、もちろん加速度運動していない座標系では慣性の法則は成り立つ。
　
　ここで多くの学生に混乱を引き起こす、やっかいな物理用語を紹介しよう。
　大地に静止している座標系で運動方程式を立てる際には、慣性力(見かけの力)\( (-m\vec{A}) \)など要らない。慣性力を入れずに運動方程式の成り立つ座標系を(何と！)慣性系という。慣性系とは、ある慣性系に対して加速度運動していない無数の座標系である。ある慣性系が例えば右向きに速度5m/sで等速運動しているならば、それに対して左向きに150,000m/sで等速運動している座標系も、斜め右下向きに270ｍ/sで等速運動している座標系も、とにもかくにも等速ならば全て慣性系である。
　一方、慣性力\( (-m\vec{A}) \)を入れて初めて運動方程式の成り立つ座標系を非慣性系という。非慣性系とは加速度座標系である（図２）。
　なぜ慣性力が必要な方を「非」慣性系と呼ぶのかと言えば、非慣性系では慣性の法則が成り立たないからだ。これに対して、慣性力が不要な方は慣性の法則が成り立つから「慣性系」と呼ぶ。