1-49-1: ケプラーの法則
ケプラーの法則はしっかり覚えましょう！ → ＜例題＞は1-49-2へ
※ ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ ケプラーの法則
第１法則 惑星の公転軌道は太陽を１つの焦点とする楕円である
第２法則 惑星の面積速度は一定である（面積速度一定の法則）
第３法則 惑星の公転周期 \(T\)、楕円軌道の半長軸(長半径)\(a\)とすると、比\(\displaystyle \frac{T^2}{a^3}\)は全ての惑星について共通の値となる
ケプラーの法則は惑星の公転運動についての法則で、17世紀初頭にケプラーが提唱した。ティコ・ブラーエという天文学者の集めた惑星に関する膨大な観測データをケプラーが分析して、3つの法則に集約させたものだ。ただし、ケプラーはその法則が何で成り立つのかの証明はしていない。時が下って17世紀後半、ニュートンはニュートンの運動の法則・万有引力の法則を提唱し、それらを組合わせてケプラーの法則を事実上証明してしまう。証明は大学教養課程レベルの「ケプラー問題」で習うことができる。
一方、高校物理としては、ケプラーの法則に現れる楕円運動が数学的にレベルが高すぎるということで、証明は通常扱わない（まれに誘導付きで法則の導出を問う問題も見られるが）。よって、ケプラーの法則は単純に覚えればよい。
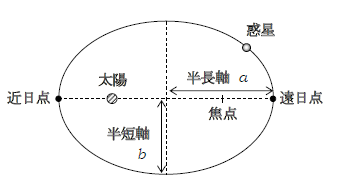
1⃣ 第１法則: 惑星の公転軌道は太陽(の中心)を１つの焦点とする楕円である。
図１を見ての通りの法則である。楕円の２つの焦点のうち、一方に太陽が位置し、他方には特に何もない。太陽から最も近い点を近日点、最も遠い点を遠日点という。楕円の長い方の軸を長軸、短い方を短軸、それぞれの半分の長さを半長軸(長半径)\(a\)、半短軸(短半径)\(b\)という [ \(a\)は英語のaxis（軸という意味）の頭文字と思われる ]
2⃣ 第２法則: 惑星の面積速度は一定である。
第2法則は別名「面積速度一定の法則」とも呼ばれる。ここで面積速度とは、惑星と太陽を結ぶ線分「動径」(図２の\(\vec{\rho}\))が、惑星が公転運動するにつれて描き出す面積（図２の扇形のような斜線部分）の単位時間あたりの量のことである。 (＊)
図２では\(\Delta t\)を微小な時間に取ってあり、しがって速度\(\vec{v}×\Delta t\)は微小な距離PQを大きさとするベクトルである。すると、斜線部分の面積と⊿PQOの面積との食い違い(図で黄色で囲った部分)は、PQが微小であるがゆえに無視できる。すなわち、(斜線部分の面積)=(⊿PQOの面積)（\(\Delta t \rightarrow 0\)のとき）としてよい。⊿PQOの底辺QO=\(\rho\)、高さPR=\(v \Delta t\sin\theta\)だから、すぐ上の(＊)より
面積速度=\(\displaystyle \lim_{\Delta t \rightarrow 0} \)(斜線部分の面積)/\(\Delta t\)\(\displaystyle =\lim_{\Delta t \rightarrow 0} \)(⊿PQOの面積)/\(\Delta t\)
\(\displaystyle =\lim_{\Delta t \rightarrow 0} \frac{1}{2}\rho v\Delta t\sin\theta/\Delta t=\)\(\displaystyle \frac{1}{2}\rho v\sin\theta\)
ここで\(\theta\)とは動径\(\vec{\rho}\)と速度\(\vec{v}\)のなす角である（図２の状況では \(\theta>90^°\)）。また、幾何学的には面積速度とは、動径\(\vec{\rho}\)と速度\(\vec{v}\)のつくる三角形の面積（⊿PQOの面積÷\(\Delta t\)）である。
さて、この面積速度が一般の物体の運動について一定である必要は必ずしもないのだが、定点(太陽の中心)からの万有引力の下、質点(惑星の中心)が運動するような場合は一定である。なぜか？その証明は、この単元の冒頭で述べた通り、大学の「ケプラー問題」に委ねておけばよい。
例えば図３で、近日点の面積速度＝遠日点の面積速度
\(\displaystyle \frac{1}{2}r_1v_1\sin90^°=\frac{1}{2}r_2v_2\sin90^°\)
が成り立つ。ここで \(r_1＜r_2\)だから\(v_1＞v_2\)。ちなみに、惑星は 近日点で最も速く、遠日点で最も遅い。
3⃣ 第３法則 惑星の公転周期 \(T\)、楕円軌道の半長軸(長半径)\(a\)（再び図１）とすると、比\(\displaystyle \frac{T^2}{a^3}\)は全ての惑星について共通の値となる。すなわち、
\(\displaystyle \frac{T_{水星}^2}{a_{水星}^3}=\frac{T_{金星}^2}{a_{金星}^3}=\cdots=\frac{4\pi^2}{GM_{太陽}}\) [ 太陽は定点と見なす ]
この証明は大学の「ケプラー問題」に委ねておけばよい。なお、(楕円運動ではなく)等速円運動という特別の場合に、第３法則を簡易的に証明した説明が1-48-2にある。
第３法則の\(\frac{4\pi^2}{GM_{太陽}}\)という値は全ての惑星に共通である。一方、第２法則で面積速度が一定値を取り続けるというというときの値は、それぞれの惑星ごとに決まっている、すなわち惑星ごとには異なる。
実はケプラーの３つの法則は、太陽の周りを回る惑星について成り立つだけではなく、非常に大きな質量を持つ物体(典型的に天体)の万有引力の下で、他の物体が閉軌道を描く場合について一般に成り立つ（その証明は大学の「ケプラー問題」に委ねよう）。例えば地球の周りを回る人工衛星、例えば木星の周りを回る衛星、など。これらはよく入試の題材になる。
また、周回する物体(惑星、人工衛星、衛星、など）の力学的エネルギーの大小によって、楕円軌道のみならず、双曲線軌道や放物線軌道を描いたりもする。そう、「ケプラー問題」の軌道は２次曲線(円錐曲線)なのである。