1-40-1: 剛体のつり合い ＜例題＞

さっそく剛体のつり合いの例題を解いてみましょう！　　　　　

例題　

　図のように、長さ\(L\)、質量\(m\)の一様でまっすぐな棒ABが、台の上にその一部分がはみだして置かれている。このとき、A端から長さ\(l\)だけ離れた点Pが台の端に当たっている。棒のA端にばね定数\(k\)のばねをつけて鉛直上方に引っ張ると、ばねが\(a\)だけ伸びたとき点Pが台の端を離れた。ただし、台の上の面は十分にあらくて棒は台に対してすべらないとする。また、重力加速度の大きさを\(g\) と、\(\displaystyle l<\frac{L}{2}\)とする。

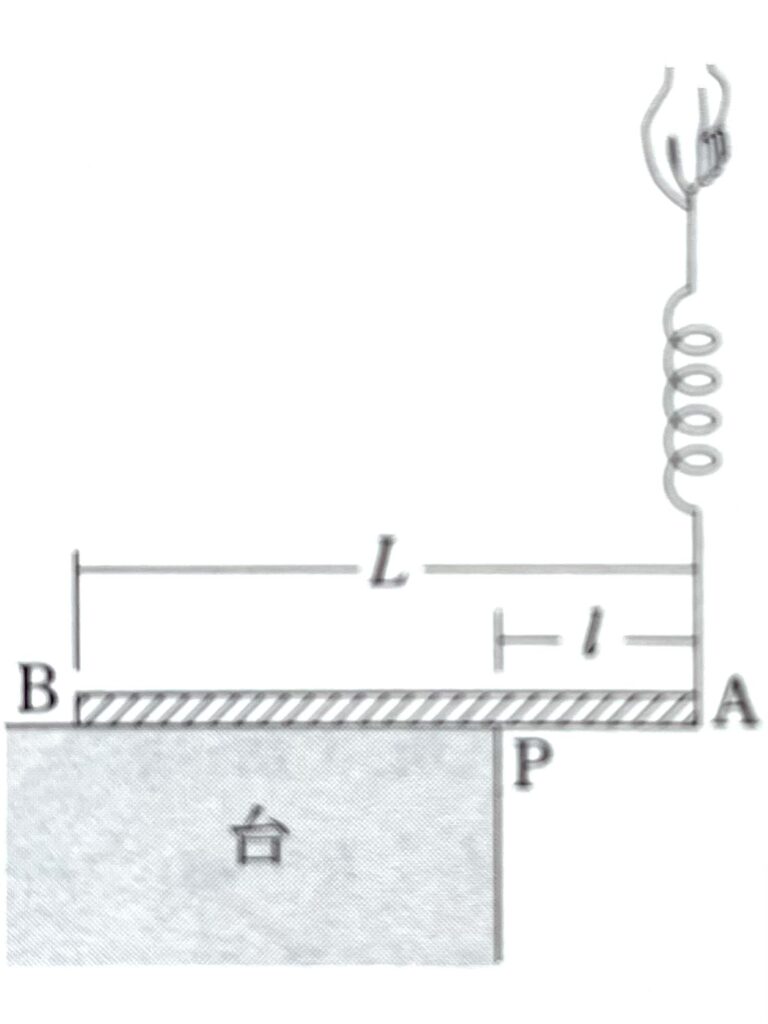
問１　この棒の質量\(m\)を表す式として正しいものを、次の➀～⑥のうちから一つ選べ。
①　\(\displaystyle \frac{2ka}{g}\)　②　\(\displaystyle \frac{ka}{g}\)　③　\(\displaystyle \frac{ka}{2g}\)　④　\(\displaystyle \frac{2ka^2}{gL}\)　⑤　\(\displaystyle \frac{ka^2}{gL}\)　⑥　\(\displaystyle \frac{ka^2}{2gL}\)
問２　次にばねをA端からはずし、B端につけかえて鉛直上方に引っ張ると、ばねが\(b\)だけ伸びたときにB端が離れた。\(b\)は\(a\)の何倍か、正しいものを、次の➀～⑥のうちから一つ選べ。
①　\(\displaystyle \frac{L-l}{L+l}\) 　②　\(\displaystyle \frac{L-l}{L+2l}\)　③　\(\displaystyle \frac{L-2l}{L-l}\)　④　\(\displaystyle \frac{L-2l}{L+l}\)　⑤　\(\displaystyle \frac{L-2l}{L}\)　⑥　\(1\)

解答・解説

　今まで通り、まず軸と力、次に\(ma=F\) と行けばよいのだが、ただし剛体では、\(ma=F\)の代わりに、モーメントと力のつり合いの式を立てる。
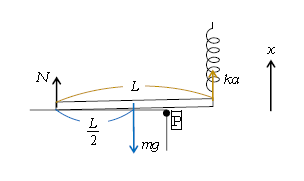
問１　棒が点Pからわずかだけ浮いた状況を考えるとよい（図１）。
　モーメントのつり合い　\(\displaystyle 0=kaL-mg\frac{L}{2}\)　　　　　　　　　(1)
　力のつり合い　\(0=N+ka-mg\:\)　　　  　　　　　　　　 (2)
　(1)より　\(\displaystyle m=\frac{2ka}{g}\:\,\)　　　　　　　　　　　　　　　　　　　(3)　　　　答　①
・　なお、(2)は\(N\)を求めるための式ということになる。

問２　棒が点Bからわずかだけ浮いた状況を考えるとよい。モーメントの中心は点P。
　モーメントのつり合い　\(\displaystyle 0=mg\left(\frac{L}{2}-l\right)-kb(L-l)\)　　(4)
　力のつり合い　\(\displaystyle 0=N’+kb-mg\)　　　　　　　　　　　　(5)
　(3)を(4)に代入　\(\displaystyle 0=2ka\left(\frac{L}{2}-l\right)-kb(L-l)\)
　\(k\)を約して　\(b(L-l)=a(L-2l)\)　　[ 選択肢を意識しながら、式変形しよう ]
　∴　\(\displaystyle b=a×\frac{L-2l}{L-l}\)　　　　答　①