1-25-1: 斜面上の単振動 ＜例題＞

この例題１つで単振動のここまで（1-22-1,1-23-1,1-24-1,1-24-2）の総まとめができます。少し長い単元ですが、頑張りましょう！　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

例題　

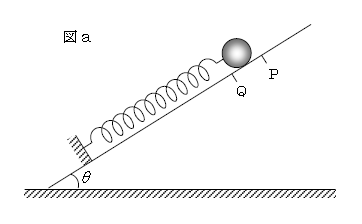
　図aのように水平面に固定された傾角\(\theta\)のなめらかな斜面がある。ばね定数\(k\)の軽いばねの一端を斜面上の壁に固定し、他端に質量\(m\)の物体をつなぐ。物体はつねに斜面上にあるものとし、以下で位置とはばねと物体のつなぎ目の位置を指す。図aでは、ばねの自然長の位置Pからばねがある距離だけ縮んだ位置Qに、外力を加えることなく物体が静止している。重力加速度の大きさを\(g\)とする。
問１　PQ間の距離を求めよ。

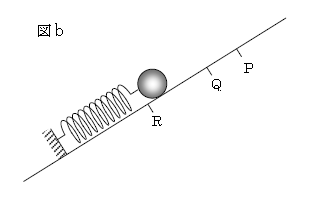
　次に、図bのように位置RをQR間の距離がPQ間の距離の2倍と等しくなるように取る。物体を位置Rに手で支えながら移し、次いで静かに手を離すと物体は単振動をした。位置Qから斜面に平行に上向きに取った変位を\(x\)とする。
問２　\(x\)だけ変位した位置で物体に加わる合力を求めよ。
問３　初めて位置Qに達したときの物体の速度を求めよ。
問４　物体が位置Rから初めて位置Qに達するまでの時間を求めよ。
問５　初めて位置Pに達したときの物体の速度を求めよ。
問６　物体が位置Rから初めて位置Pに達するまでの時間を求めよ。

解答・解説

　単振動のありとあらゆる問題を、1-24-1のポイントの手順に従って考えていくことが単振動攻略の早道だ。

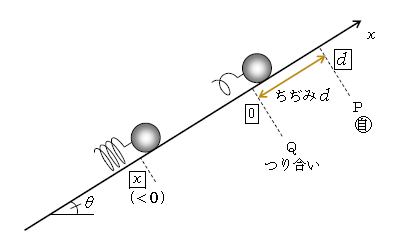
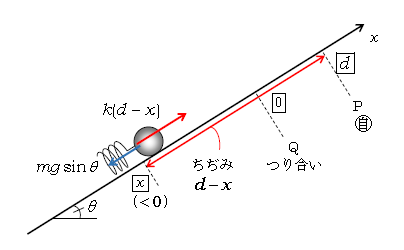
　まず軸と力の図示。\(x\)軸に正の向き、原点、自然長の位置、つり合い点\(x_c\)を添え、さらに\(x_c\)及び任意の位置\(x\)に物体を書く。いまつり合い点はQで、Qを原点に取る(\(x_c=0\))（図１。座標には□印の囲みを入れてある）。Pの下に〇印で自とあるのは自然長の位置という意味。自然長からのちぢみを\(d\)とおけば、縮んだ所が原点のQだから、Pの座標は\(d\)になる。次に任意の\(x\)であるが、のび・ちぢみの一方だけ調べればよく（1-22-1）、いまちぢみ側に\(x\)(<0)を取った（図１）。

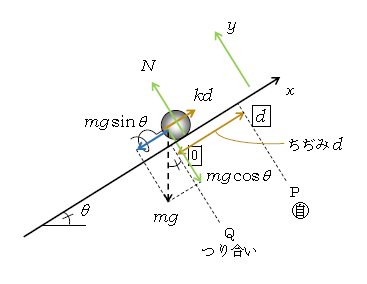
問１　つり合い点Qで力を図示する（図２）。まず重力\(mg\)を下向きに書いて、次に物体にふれているものを探す。物体に斜面がふれているから、斜面から働く垂直抗力\(N\)を斜面に垂直に書く。物体にばねがふれているから、ばねから働く弾性力を書く。弾性力の向きは縮んだばねが自然長に戻ろうとして物体を押す(斜面に沿って上)向き。弾性力の大きさは\(k\)×ちぢみ\(=kd\) 。
　次に\(ma=F\)　つり合いの式を\(x\)、\(y\)方向について立てるために、\(mg\)を分解。\(x\)方向に\(mg\sin\theta\)、\(y\)方向に\(mg\cos\theta\)（図２）。
　つり合い：(\(x\)成分) \(0=kd-mg\sin\theta\)　　　　(1)
　∴　\(d=\overline{\text{PQ}}=\)　答　\(\displaystyle \frac{mg}{k}\sin\theta \)
　・　なお、問では聞かれていないが、つり合い：(\(y\)成分) \(0=N-mg\cos\theta\)　　

問２　再びまず軸と力に戻って、任意の\(x\)で力を図示する。今度は\(x\)方向の力だけ書いた（図３）。ばねのちぢみとは自然長からのずれ\(|d-x|\)で、斜面に沿って上向きを正に取ったということは、上側の座標\(d\)の方が下側の座標\(x\)より大きい。ゆえにちぢみは大きい方から小さい方を引いた\(d-x\)で、弾性力の大きさは\(k(d-x)\)。
　次に\(ma=F\)　[ 図３を見ながら ]
　\(ma=k(d-x)-mg\sin\theta=-kx+kd-mg\sin\theta\)　[ (1)を用いて ]
　　　\(=-kx\)　　　　　　　　　　　　　　　　　(2)　　　　　　　　　
　求める合力とは\(ma=F\)の\(F\)だから　答　\(-kx\)

　1-24-1のポイントに従って続きを書くと、(2)の両辺を\(m\)で割って　
　　　　　　　　\(\displaystyle (a=)\frac{d^2x}{dt^2} =-\frac{k}{m} (x-0) \)
　これを単振動の方程式 \(\displaystyle \frac{d^2x}{dt^2} =-\omega^2 (x-x_c) \)　と比べて
　 \(\omega\) \(\displaystyle =\sqrt{\frac{k}{m}} \) 、 \(x_c\) \(=0\) を読み取る。\(\,\) 　　　　　 (3)
　（原点をつり合い点Qに取ったのだから、\(x_c=0\)になるのは当然）
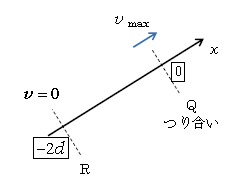
問３　運動\(v,x\)を調べる　初期条件\(v_0,x_0\)に注意する。いま初期位置R（図４）にて\(v_0=0\)、\(x_0=-2d\)。すると1-24-2で扱った「つり合い点から\(-2d\)ずらして静かに離す」パターンになるから、
　\(x=-2d\cos\omega t\)　　　　　　　　　　　　　　　(4)
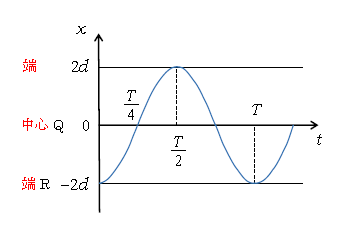
であると分かる（グラフは図５）。ここまでで、1-24-1のポイントの手続きは完了。
　さて、求めるQでの速度をエネルギー保存則で計算することもできる。しかしQはつり合い点だから、1-24-2の公式
　つり合い点にて\(v_{\text{max}} =A\omega\)　　　　　　　　　　 (5)
が便利。ここで\(A\)は振幅で、図５より\(A=2d\)。よって(3)の\(\omega\)を用いて
　\(v_{\text{max}} =\)　答　\(\displaystyle 2d\sqrt{\frac{k}{m}} \)

問４　1-23-1の通り、周期\(\displaystyle T=\frac{2\pi}{\omega}=2\pi \sqrt{\frac{m}{k}} \: \)　 (6)　　[ (3)を用いた ]
　図５よりQまでの時間は \(\displaystyle \frac{T}{4}= \)　答　\(\displaystyle \frac{\pi}{2}\sqrt{\frac{m}{k}} \)
・　単振動でよく聞かれる時間としては、
　振動の　端～中心\(\displaystyle =\frac{1}{4} \)周期　[ 図５の赤字を見よ ]
　　　　一端～他端\(\displaystyle =\frac{1}{2} \)周期　
がある。これらは、即座に答えられるようにグラフのイメージを頭に焼き付けておこう。
問５　Pは自然長の位置でつり合い点ではないから、公式\(v_{\text{max}} =A\omega\)は使えない。その代わりに力学的エネルギー保存則：
　　運動エネルギー\(\displaystyle \frac{m}{2}v^2\)＋重力による位置エネルギー\(mg\)×(高さ)
　　＋弾性エネルギー\(\displaystyle \frac{k}{2}\)×(のび・ちぢみ)\(^2\)＝一定　　を用いるのが手早い。
　図６の高さやちぢみを見ながら　　
　　　　　　　　あと　　　　　　　　　　　　 まえ
　\(\displaystyle \frac{m}{2}v’^2+mg×3d\sin\theta+ \frac{k}{2}0^2 = \frac{m}{2}0^2+mg0+ \frac{k}{2}(3d)^2 \)
　　左辺第2項\(=mg\sin\theta×3d=kd×3d \)　[ (1)を用いた ]　と書き換えると、
　\(\displaystyle \frac{m}{2}v’^2=\frac{k}{2}(3d)^2 -3kd^2=\frac{3}{2}kd^2 \)　　両辺\(\displaystyle \frac{2}{m} \)倍して \(\displaystyle v’^2=\frac{3k}{m}d^2 \)
　よって \(v’=\)　答　\(\displaystyle d\sqrt{\frac{3k}{m} } \)
問６　時間は\(x\)と\(t\)の関係(4)で求める。Pまでの時間を\(t’\)とすると、Pでの\(x=d\)だから、(4)より
　\(x=d=-2d\cos\omega t’\)　　∴　\(\displaystyle \cos\omega t’=-\frac{1}{2} \)　　∴　\(\displaystyle \omega t’=\frac{2\pi}{3},\frac{4\pi}{3},\cdots \)
　問題文に「初めてPに達する時間」とあるから、時間\(t’\)の最小値を求めればよい。
　∴　\(\displaystyle \omega t’=\frac{2\pi}{3} \)　　∴　\(\displaystyle t’=\frac{2\pi}{3}\frac{1}{\omega} \)　[ (3)を用いて ]　答　\(\displaystyle \frac{2\pi}{3}\sqrt{\frac{m}{k}} \)

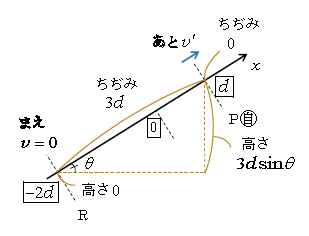
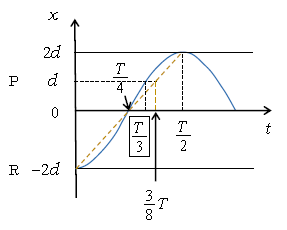
・　結局 \(\displaystyle t’=\frac{2\pi}{3}\frac{1}{\omega}=\frac{1}{3}\frac{2\pi}{\omega}=\frac{1}{3}T \) である（図７）。
　　グラフが仮に直線(図７黄色の点線)だったならば、求める時間は \(\displaystyle \frac{3}{8}T\)となる。ただし、単振動のグラフは曲線(三角関数)だから、直線的なイメージは誤りである。
・　単振動で時間を求めさせるときは、\(\sin\omega t\)あるいは\(\cos\omega t\) が \(\displaystyle \frac{1}{2},\frac{\sqrt{2}}{2},\frac{\sqrt{3}}{2},\cdots\) のような「キリのいい数」になる場合しか出題されない。
・　時間を求めさせる問題のほとんど全てで、\(x\)と\(t\)の関係は1-24-2の通り\(\pm \sin\)型や\(\pm \cos\)型となる。ただし、ごくまれにそうならない（\(\sin (\omega t+\phi)\)のようになる）出題がある。その場合の対策はここでは深入りしない。