1-21-1: 非等速円運動

速さの変わっていく「非」等速円運動をきっちりマスターしましょう !　→　＜続き＞は1-21-2へ　　　　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

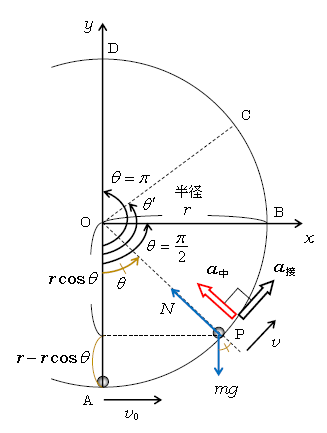
　非等速円運動の例として、小球が鉛直面内をなめらかな円形レールの内側に沿って動く図１を扱う。「鉛直面内」ということは、天井から見下ろした図ではなく、真直ぐ立ったレールを真横から見ているという意味。
　図の点Aは最下点で、球に初速度\(v_0\)を水平右向きに与える。Aから左回りに中心角\(\theta\)を測る。点Pは任意の\(\theta\)の位置で、速さ\(v\)、加速度の中心成分\(a_中\)(中心に向かう向き正)、接線成分\(a_接\)(\(\theta\)の増える向き正)とあり、球に加わる重力\(mg\)と垂直抗力\(N\)も書かれている。点Bは\(\theta=\frac{\pi}{2}\)の位置、点Cは球がレールから離れる可能性のある位置、点Dは最高点である。
　非等速円運動には鉄則のようなものがあり、ズバリ以下の連立を解く。
　力学的エネルギー保存 　　　　　　　　　　　　 (I)
　運動方程式の半径方向成分（円運動の方程式）　 (II)　（1-20-1）

　(I)は点Pをあと状態、点Aをまえ状態かつ高さ0に取って（図１）
　　　　　　 あとP　　　　　　=　　　まえA
　　\(\displaystyle \frac{m}{2}v^2+mg(r-r\cos\theta) =\frac{m}{2}v_0^2+mg0 \)　　　　　(i)
　(II)は　\(\displaystyle ma_中=m\frac{v^2}{r} =F_中 \)（合力の半径方向成分、中心向き正）、すなわち
　　\(\displaystyle\)\(\displaystyle m\frac{v^2}{r} =N-mg\cos\theta \)　　　　　　　　　　　　　　 (ii)
　\(F_中\)には\(N\)だけでなく、中心向きを正に\(-mg\cos\theta\)も入ってくることに注意。

　(i)からは\(v^2\)が(つまり実質\(v\)が)\(\theta\)の関数として求まる。
　　\(v^2=v_0^2-2gr+2gr\cos\theta \)　　　　　(1)
　これを(ii)に代入すると\(N\)が\(\theta\)の関数として求まる。
　　\(\displaystyle N=\frac{m}{r}v^2 +mg\cos\theta \)
　　　 \(\displaystyle =\frac{m}{r}(v_0^2-2gr+2gr\cos\theta) +mg\cos\theta \)
　　　 \(\displaystyle =\frac{mv_0^2}{r}-2mg+3mg\cos\theta \)　　　(2)
　この(1)、(2)に基づいて次の1-21-2で詳しいを考察していく。が、その前に、運動方程式の接線方向成分は（図１）
　　\(ma_接=-mg\sin\theta \)　　∴　\(a_接=-g\sin\theta \)　　
　例えば加速度の大きさ\(a\)はと聞かれたら、\(\displaystyle a_中=\frac{v^2}{r}\) を答えるのではなく、
　\(a=\sqrt{(a_接)^2+(a_中)^2} \) を答える。\(a_接\)も含めなければいけないので要注意だ。