1-21-2: 非等速円運動(続き)
非等速円運動には3つの典型的な運動パターンがあります。
ポイント
(a) \(0<v_0≦\sqrt{2gr}\) → \(\displaystyle |\theta|≦\frac{\pi}{2} \)の範囲でレールに沿って往復運動
(b) \(\sqrt{2gr}<v_0<\sqrt{5gr}\) → \(\displaystyle \frac{\pi}{2}<\theta<\pi \)のどこかでレールを離れて放物運動
(c) \(v_0≧\)\(\sqrt{5gr}\) → レールを回転運動し続ける
1-21-1の(1)、(2)式を再掲しておく。
\(v^2=v_0^2-2gr+2gr\cos\theta \, \) (1)
\(\displaystyle N=\frac{mv_0^2}{r}-2mg+3mg\cos\theta \) (2)
上のポイント欄にまとめた(a)、(b)、(c)の順に解説していこう。
(a) 手始めに、\(v=0\)となる\(\theta=\alpha\)としてみる。(1)より
\(v^2=0=v_0^2-2gr+2gr\cos\alpha \)
∴ \(\displaystyle \cos\alpha=1-\frac{v_0^2}{2gr} \) ①
これを(2)に代入
\(\displaystyle N=\frac{mv_0^2}{r}-2mg+3mg\cos\alpha\)
\(\displaystyle =\frac{mv_0^2}{r}-2mg+3mg\left(1-\frac{v_0^2}{2gr} \right) \)
\(\displaystyle =mg-\frac{mv_0^2}{2r}\) ②
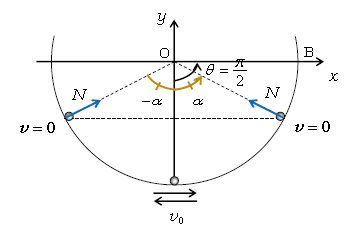
ここで気付くことがある。\(v_0<\sqrt{2gr}\)なら①より \(\cos\alpha>0\)だから(\(v=0\)となる)\(\alpha<\frac{\pi}{2}\)。また②より\(N>0\)。\(N\)は球とレールが接触して初めて働く力だから、\(N>0\) ということは球とレールが離れていないことを意味する。すると図1のように、\(\alpha\)でいったん静止した球は、レールから離れることなく左向きへ移動し、同じ高さの\(\theta=-\alpha\)の位置まで行って再び静止する。なぜなら、同じ高さの位置(\(\alpha\)と\(-\alpha\))では位置エネルギーどうしが等しく、力学的エネルギー(運動エネルギーと位置エネルギーの和)一定により運動エネルギーどうしも等しいから、ともに\(v=0\) である。こうして、\(v_0<\sqrt{2gr}\)なら\(-\alpha≦\theta≦\alpha\)の範囲でのレールに沿った往復運動が実現する。
なお、\(v_0=\sqrt{2gr}\)のときは、①より\(v=0\)となる\(\cos\alpha=0\)つまり\(\alpha=\frac{\pi}{2}\) 。②より\(N=0\) 。ゆえに\(\alpha=\frac{\pi}{2}\)で一瞬\(N=0\)になるが、一瞬だけ\(N=0\)になってもレールから離れていることを目視できるはずもない。 (☆)
よって\(v_0≦\sqrt{2gr}\)までなら往復運動で、図1の\(\alpha≦\frac{\pi}{2}\)の範囲である。
(b) 次に\(v_0>\sqrt{2gr}\)なら、①より \(\cos\alpha<0\)だから(\(v=0\)となる)\(\alpha>\frac{\pi}{2}\)。また②より\(N<0\)。しかし垂直抗力の「大きさ」\(N<0\)などあり得ない。球がレールから離れていないと「仮定」して求めた\(N\)が<0と求まったのは矛盾で、背理法により仮定の逆、つまり球はレールから離れている。というわけで、\(v=0\)となるはずの\(\alpha\)(\(>\frac{\pi}{2}\))では既に球はレールから離れているのだ。
そこで今度は\(N=0\)となる\(\theta=\theta’\)としてみよう。(2)より
\(\displaystyle N=0=\frac{mv_0^2}{r}-2mg+3mg\cos\theta’ \)
∴ \(\displaystyle \cos\theta’=\frac{2}{3}-\frac{v_0^2}{3gr}\) ③
これを(1)に代入
\(\displaystyle v’^2=v_0^2-2gr+2gr\left(\frac{2}{3}-\frac{v_0^2}{3gr}\right) =\frac{1}{3}v_0^2-\frac{2}{3}gr \) ④
するとまた気付く。\(v_0>\sqrt{2gr}\)なら③より \(\cos\theta'<0\)だから(\(N=0\)となる)\(\theta’>\frac{\pi}{2}\)。また④より\(v’^2>0 \)。よって図2のように、小球は\(\theta’>\frac{\pi}{2}\)のどこかでレールを離れ(\(N=0\))、初速度\(v’\)の放物運動をする。
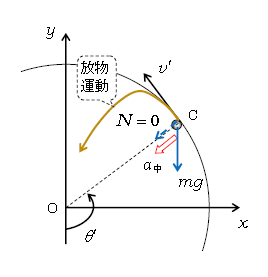
結局のところ、なぜレールを離れるのかと言えば 、\(\theta\)が増える → 高さが増える → 位置エネルギーが増える → 力学的エネルギー(運動エネルギーと位置エネルギーの和)一定により運動エネルギーが減る → \(v\)が減る → \(a_中=\frac{v^2}{r}\)が減る → \(ma_中=F_中\)により\(F_中\)が減る → 中心向きの力\(N\)が減る → ついに\(N=0\)になると離れる、というわけである。
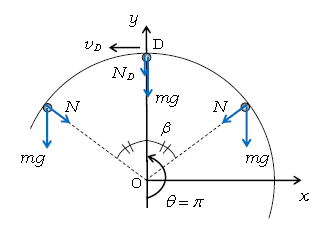
(c) 引き続いて、最高点D(\(\theta=\pi\))をレールから離れることなく通過する条件を求めてみよう(図3)。点Dで\(v_D>0\)かつ\(N_D≧0\)ならばよい。[ 最高点で一瞬だけ\(N_D=0\)になるのは、(☆)で述べた通り問題ない。また、\(\cos\theta\)が\(\theta\)の減少関数であることに注意すると、(1)(2)より\(v\)、\(N\)は\(\theta\)の減少関数だから、\(\theta=\pi\)(点D) での\(v_D>0\)、\(N_D≧0\)ならば、\(0≦\theta<\pi\)全ての\(v>v_D>0\)、\(N>N_D≧0\)である。]
(1)より \(v_D^2=v_0^2-2gr+2gr\cos\pi>0 \) ∴ \(v_0^2>4gr \)
(2)より \(\displaystyle N_D=\frac{mv_0^2}{r}-2mg+3mg\cos\pi>0 \) ∴ \(v_0^2≧5gr \)
この2行分の式より\(v_0^2≧5gr \)なら(\(v_0^2>4gr \)も自動的に成り立ち)最高点Dを通過する。点Dを通過する前と通過した後の、角度が例えば\(\beta\)どうしで等しい場所は明らかに線ODに関して線対称性があるから(図3)、通過前の運動と線対称な運動が通過後には実現する。[ ただし、速度の向きのことは忘れて、速度の大きさ(速さ)をイメージする。] よって、小球は\(v_0≧\sqrt{5gr} \)ならレールに沿って回転運動し続ける。
以上の非等速円運動における3つの運動パターンは入試で頻出なので、ハナから覚えておくぐらいがよい。
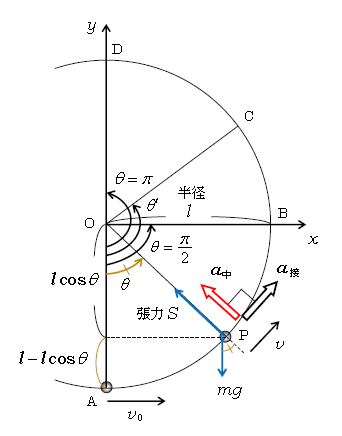
なお、3つの運動パターンは、長さ\(l\)の軽い糸につながれた小球の鉛直面内の非等速円運動にも通用する(図4)。
(a’) \(0<v_0≦\sqrt{2gl}\) → \(\displaystyle |\theta|≦\frac{\pi}{2} \)の範囲で往復運動
(b’) \(\sqrt{2gl}<v_0<\sqrt{5gl}\) → \(\displaystyle \frac{\pi}{2}<\theta<\pi \)のどこかで糸がたるんで放物運動
[ 張力\(S=0\)になると糸はたるむ。逆に\(S>0\)のときは糸はピンと張っている。]
(c’) \(v_0≧\sqrt{5gl}\) → 回転運動し続ける