1-30-1: 相対速度とはね返り係数
ここでいよいよ2物体の衝突現象に入っていきます。 → 2次元の相対速度・加速度 <例題> は1-30-2へ
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ 観測者Pの速度、加速度をそれぞれ\(v_P, \, a_P \)、
物体の速度、加速度をそれぞれ\(v, \, a \)として
Pから見た(Pに対する)物体の相対速度 \(v’=v\)\(-v_P\)
Pから見た(Pに対する)物体の相対加速度\(a’=a\)\(-a_P\)
・ 物体1、2の衝突直前の速度をそれぞれ\(v_1, \, v_2 \)、
衝突直後の速度をそれぞれ\(v’_1, \, v’_2 \)、
はね返り係数(または反発係数)を \(e\) とすると、
\(v’_1 – v’_2 =-e(v_1 – v_2) \)
・ \(e=1\) のときを(完全)弾性衝突
\(0≦e<1 \, \) のときを非弾性衝突
\(e=0\) のときを完全非弾性衝突 という
・ 斜衝突でのはね返り係数は、衝突面に垂直な速度成分で定義する
通常、物理で物体の速度というときには、観測者(人)は大地や床の上で静止しながら物体を見ている。一方、電車に乗りながら飛んでいる鳥を見ると、鳥本来の速度よりもゆっくり飛んでいるように見えたりする(電車と鳥が同じ向きに動いているならば)。これを電車(に乗っている人)から見た鳥の相対速度という。つまり相対速度とは、動いている観測者から見た速度である。通常の速度を\(v\)で表すとき、相対速度にはダッシュ(')を付けて\(v’\)のように表すことにしよう。
図1で物体が1sあたり15m進んでいるならば物体の速度は\(v=\)15m/s。一方、その間に観測者Pが5m進んでいるとするとPの速度\(v_P=\)5m/s。1s後のP(右側のP)から見ると物体は10mだけPから離れていくように見えるから、
Pから見た(またはPに対する)物体の相対速度\(v’=v-v_P\) =10m/s
であると分かる。Pから見た相対速度では\(v_P\)を引き算するのだから、「から見た」(に対する)を引き算する公式と覚えよう。 [ 厳密には、1s間速度が一定のままの場合に今の説明は成り立つ。1sの間に速度が変化するときは、速度の変化が無視できるくらい短い微小時間\(\Delta t\)に話を限定し、図1の矢印を\(v\Delta t \, , v_P\Delta t \, , v’\Delta t\) と書き直す必要がある。 ]
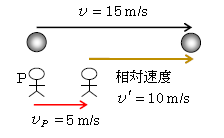
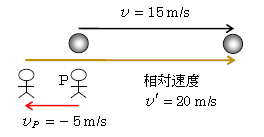
図2のように、物体と観測者Pの動きが逆向きの場合も同様。つまり、1s後のP(左側のP)から見て物体は20=15-(-5) m離れていくように見えるから、\(v’=v-v_P \)の公式はやはり成り立つ。
同様に相対加速度とは動いている観測者から見た加速度のこと。例えば物体の速度が1sあたり15m/s増加中なら物体の加速度は\(a=\)15m/s\(^2\)。一方、その間に観測者Pの速度が5m/s増加しているならPの加速度\(a_P=\)5m/s\(^2\)。物体の速度が15m/s増える間にもPの速度が5m/s増えるということは、1s後のPから見て物体の速度は相対的に15-5=10m/sしか増えない。これを相対加速度10m/s\(^2\)という。
Pから見た物体の相対加速度\(a’=a-a_P\) =10m/s\(^2\) やはり「から見た」を引き算する。
はね返り係数
ここで物体1,物体2どうしが衝突してはね返る現象を考えよう。 (☆)
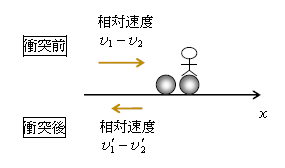
図3で\(x\)軸上を直線運動する物体1、2の衝突直前の速度がそれぞれ\(v_1, \, v_2 \)、衝突直後の速度はそれぞれ\(v’_1, \, v’_2 \)であるとする。 [ ここでダッシュ(')を付けたのは、動いている観測者から見た相対速度という意味ではなく、あくまでも大地や床の上で静止している観測者から見た通常の速度で、ただし衝突直後の速度という意味である。]
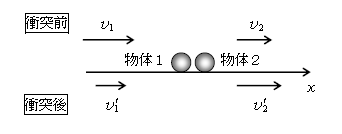
さて、これをあたかも物体2とともに動く観測者から見たのが図4。
衝突直前の2から見た1の相対速度は、「2から見た」を引き算して\(v_1 – v_2\) 。衝突が起きるためには物体1が2に追いつかなければならないから図3の\(v_1 > v_2\)、つまり\(v_1 – v_2 >0\)である。これは、衝突前は2から見て1は\(x\)軸の正の向きに動く、2から見て1は近づくという意味。
衝突直後の2から見た1の相対速度は\(v’_1 – v’_2\) (図4)。衝突後はね返るためには図3の\(v’_1 < v’_2\)(逆に\(v’_1 > v’_2\)なら衝突後に物体1が2を追い越しているという意味になり、これは1が2を突き破るか何かしているということ。(☆)で述べた1と2どうしがはね返る状況としては不適である)。すると\(v’_1 – v’_2<0\)、つまり衝突後は2から見て1は負の向きに動く、2から見て1は遠ざかる。
ここで衝突直後の相対速度\(v’_1 – v’_2\)が、衝突直前の相対速度\(v_1 – v_2\)の(\( – \))何%に相当するかを考えて、何%にあたる量をはね返り係数(または反発係数) \(e\) という。
\(v’_1 – v’_2 =-e(v_1 – v_2) \) (*)
例えば\(e\)=0.3(30%)とは、直後の相対速度が直前の0.3倍の大きさの「はね返り方の度合い」であるという意味。\(e\)の手前にマイナスをつける理由は、\(v_1 – v_2>0\)に対して\(v’_1 – v’_2<0\)だから、つまり、物体2から見て1は衝突前近づくのに衝突後は遠ざかるからである。
なお、\(v’_2 – v’_1 =-e(v_2 – v_1) \) と表した式は(*)と同値だから、物体1の方で引き算してもかまわない。
\(e\)の値には2物体の材質などいろいろな要因が関わってくる。例えば鉄と銅の衝突だと\(e\)は1近くになり、木片と粘土の衝突だと\(e\)は0に近いといった具合。
\(e=1\) のときを弾性衝突(または完全弾性衝突)という。
\(0≦e<1 \, \) のときを非弾性衝突という。
\(e=0\) のときを完全非弾性衝突という。(*)式に\(e=0\)を代入すると\(v’_1\) \(= v’_2\) となることから、\(e=0\)の場合は衝突直後2物体が並走する、すなわちくっ付いてしまう。
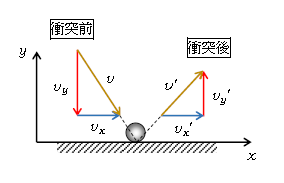
最後の話として ―― 放物運動している小球が地面に衝突するような場合、衝突面(地面)に対して斜めの方向の衝突が起こる(図5)。この斜衝突でのはね返り係数は、衝突面に垂直な速度成分で定義する。定義するとは、衝突面に垂直な成分を取ることに決めるという意味だ。すなわち図5の\(v,v’\)は用いずに、衝突面に垂直な\(y\)成分\(v_y,v’_y\)を用いる。具体的には物体1を小球、物体2を大地と見なして、(*)を
\(v’_y – 0 =-e(v_y – 0) \) [ ここで0とは大地の速度の\(y\)成分が0という意味 ]
のように立式する。図5で\(v’_y >0,\: v_y<0\)だから、この立式に何ら問題はない。特に\(e=1\)ならば\(|v’_y| =|v_y| \) 。つまり、地面のような固定面との弾性衝突では、固定面に垂直な速度成分は衝突直前・直後で不変である。