1-09-2: 摩擦力 ＜例題１＞

３種類の摩擦 ―― 静止摩擦、最大摩擦、動摩擦 ―― を使いこなして運動方程式を立てられるようにしましょう！　→　＜例題２＞は1-09-3へ

例題１　

　水平な床に質量\(m\)の物体が置かれている。図のように、物体に棒を取り付け、棒と床のなす角度を\(\theta\)として、棒の方向に大きさ\(F\)の力を加えた。ただし、棒の質量は無視できるものとし、物体と床の間の静止摩擦係数を\(\mu\)、動摩擦係数を\({\mu}’ \)、重力加速度の大きさを\(g\)とする。

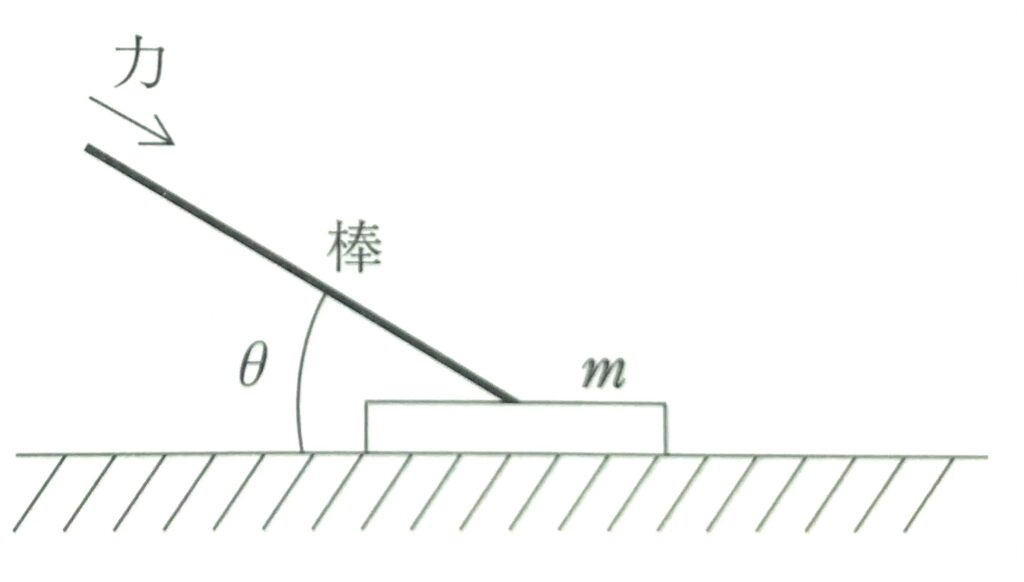
問１　\(F\)の大きさを\(F_1\)にしたところ物体は静止したままだった。このとき物体に床から働く摩擦力の大きさはいくらか。正しいものを、次の①～⑤のうちから一つ選べ。
①　\(\mu mg\) 　②　\(\mu (mg+F_1\cos\theta) \)　③　\(\mu (mg+F_1\sin\theta) \)　
④　\(F_1\cos\theta \)　　⑤　\(F_1\sin\theta \)　
　　
問２　次に、\(F\)の大きさを徐々に大きくしていったところ、その大きさが\(F_2\)を越えたとき物体が動き始めた。\(F_2\)はいくらか。正しいものを、次の①～⑧のうちから一つ選べ。
①　\(\displaystyle \frac{\mu mg}{\cos\theta -\mu \sin\theta} \)　　②　\(\displaystyle \frac{\mu mg}{\cos\theta} \)　　③　\(\displaystyle \frac{\mu mg}
{\sin\theta -\mu \cos\theta} \)　　
④　\(\displaystyle \frac{\mu mg}{\sin\theta} \)　　⑤　\(\displaystyle \frac{mg}{\cos\theta -\mu \sin\theta} \)　　⑥　\(\displaystyle \frac{mg}{\cos\theta} \)　　
⑦　\(\displaystyle \frac{mg}{\sin\theta -\mu \cos\theta} \)　　⑧　\(\displaystyle \frac{mg}{\sin\theta} \)　

解答・解説

　1-08-1: 力学攻略の基本　の流れに従って行く。
　まず軸と力を図示　物体は右向きに直線運動しようとするから、右向きに\(x\)軸、上向きに\(y\)軸。
　力は\(mg\)、ふれている棒から\(F\)、床面から「面に垂直な垂直抗力\(N\)と面に平行な摩擦力\(R\)」。

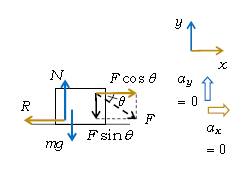
　次に\(ma=F\)　
　正の向きに、\(a_x=0\)、\(a_y=0\)と図示。\(x\)、\(y\)軸に対して斜めの\(F\)を分解。
　運動方程式は各方向ごとに別々に立てる。
　　\(x\)方向: \(m0=F\cos\theta -R \)　　　　　　　　　　　　　　　(1)　　                            
　　\(y\)方向: \(m0=N-F\sin\theta -mg \)　　　　　　　　　　　　(2)
問１　\(F=F_1\)だから、(1)より\(R=F_1\cos\theta \)　　　　答　④    
（まだ余裕ですべっていない状況だから、すべり出す直前の公式\(R=\mu N\)（1-09-1）を用いてはいけない。）
問２　\(F=F_2\)のときはすべり出す直前だから、公式\(R=\mu N \)　　(3)
を用いてよい。
　(1)より　\(R=F_2\sin\theta \)
　(2)より　\(N=mg+F_2\sin\theta \)　　[ \(N=mg\)とは限らない ]
　これらを(3)に代入　\(F_2\cos\theta =\mu(mg+F_2\sin\theta) \)　
　　∴　\(F_2(\cos\theta -\mu\sin\theta)=\mu mg \)　　∴　\(\displaystyle F_2=\frac{\mu mg}{\cos\theta -\mu\sin\theta} \)　　　
　答　①