1-24-2: 単振動のx-tグラフの4パターン ＜動画あり＞

タイトルを言い換えると、初期条件の4大パターンとも言えます。　　　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の $\equiv$ 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

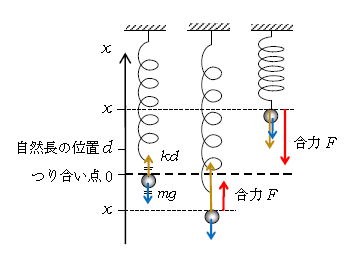
　まず準備として、「復元力」という重要な用語を解説する。図1は1-24-1図1と同様の図。つり合い点($x=0$)では弾性力(黄色)と重力(青)がつり合っている。
　物体がつり合い点の下に来ると、ばねののびが大きくなって上向きに引っ張る弾性力が下向きの重力より勝り、合力$F$(赤、弾性力と重力の合計)は上を向く。
　$\displaystyle$つり合い点の上に来ると、ばねののびが小さくなる、もしくはばねがちぢんで押しの弾性力が下向きとなり、合力$F$は下を向く。
　つまり、合力がつねにつり合い点に向いている。このタイプの合力$F$を復元力という。

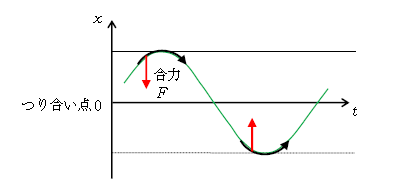
　復元力の下での運動の様子を示したのが図2。物体がつり合い点の上に来ると、「つり合い点に向く合力$F$(下向き)」でつり合い点に引き戻される。次いで、勢い余ってつり合い点を通り過ぎ下まで来ると、「つり合い点に向く合力$F$(上向き)」で再びつり合い点に引き戻される。このようなことから、つり合い点が振動(往復運動)の中心になること（それは既に1-23-1で導いている）がうなずける。

　では、いよいよ前の単元1-24-1の続き　運動$v,x$を調べる　に入ろう。これについては下の動画を見てほしい。もちろん、弾性力：黄色、重力：青、合力$F$：赤 で、$d$は自然長の位置である。

　パターン1，2：つり合い点から$\pm A$ずらして静かに離す 場合の振幅は明らかに$A$であるから、
　　$x=\pm A\cos \omega t+x_c$　であると分かる。
　一方、パターン3，4：つり合い点で初速度$\pm v_0$を与える 場合の振幅は、まず
　　公式 つり合い点$x=x_c$にて$v_{\text{max}} =A\omega$　
を押さえる。この証明には、1-23-1でやった
　$x=A\sin(\omega t+\phi)+x_c$　及び　　$v=A\omega \cos(\omega t+\phi)$
を用いる。$v$が最大値$v_{\text{max}}$となるのは、$\cos$が最大になる$\cos(\omega t+\phi)＝1$のときだから$v_{\text{max}} =A\omega$。このとき $\sin(\omega t+\phi)＝0$ [$\cos＝1$のとき$\sin＝0$] であるから$x=x_c$ 。つまり、つり合い点（振動中心）$x=x_c$にて$v_{\text{max}}=A\omega$（証明終り）。
　さて、いま初期条件$x=x_c$にて$v=\pm v_0=\pm v_{\text{max}}=\pm A\omega$（複合同順）であるから、振幅$\displaystyle A=\frac{v_0}{\omega}$ 。
　よって、$\displaystyle x=\pm\frac{v_0}{\omega}\cos \omega t+x_c$　となる。
　$v_{\text{max}}=A\omega$は便利な公式だから、ぜひ覚えておこう。