2-18-1: 全反射

屈折の法則で生じる現象として、まずは「全反射」を扱いましょう！　→　＜例題＞は2-18-2へ

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　まずは2-16-1でやった「\(n\)大きい方が\(\theta\)は小さい」ことを思い出そう。例えば水から空気へ光が入射する場合（図３）、\(n_1<n_2\)なので\(\theta_1>\theta_2 \)。屈折角\(\theta_1\)の方が入射角\(\theta_2\)よりも大きい。

　さて、入射角\(\theta_2\)を（頭の中で）大きくしてみよう、30°,40°,\(\cdots\)。屈折角\(\theta_1\)の方が大きいから\(\theta_1\)は例えば50°,70°,\(\cdots\)のようになり、入射角\(\)より先に屈折角\(\theta_1\)が90°に達する（図１）。この状況を臨界状況といい、このときの入射角を臨界角\(\theta_c\)という。

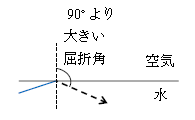
　入射角\(\theta_2\)を臨界角\(\theta_c\)よりもさらに大きくしたらどうなるだろうか。対応して屈折角\(\theta_1\)は90°より大きくなると言いたい所だが、90°より大きくなると、水から空気へ行くはずの屈折光が水に戻ってくることになる（図４）。これは屈折光とは呼べない。なぜなら、屈折光とは水から境界を乗り越えて空気へ行く光のことだからだ。つまり、もはや屈折光は存在しなくなって反射光だけになる（図２）。この現象を全反射という。

　全反射がらみで問われることは大きく分けて２つ。
1⃣　臨界角\(\theta_c\)の計算　
　これは次のようにして考えると簡単だ。臨界状況とは屈折角90°の状況（図１）だから、屈折の法則\(n× \sin\theta \)=一定　より
　\(n_1\sin90° =n_2\sin\theta_c \)　　　　(1)　　
　よって \(\displaystyle \sin\theta_c =\frac{n_1}{n_2} \) 
　この公式は別に覚える必要はない。屈折角が90° あることさえ理解できていれば、(1)よりあっという間に求まるから。

2⃣　全反射が起こるための条件
　入射角\(\theta_2\)が臨界角\(\theta_c\)よりも大きくなると全反射が起こる（図２）のだから、\(\sin\theta_2 >\sin\theta_c \)
　ところが(1)のように計算すれば　\(\displaystyle \sin\theta_c =\frac{n_1}{n_2} \)
　よって \(\displaystyle \sin\theta_2 >\frac{n_1}{n_2}\)が求める条件になる。
　なお、全反射が起きるためには、入射角\(\theta_2\)よりも屈折角\(\theta_1\)の方が大きく（図３）、入射角よりも先に屈折角の方が90° に達することが重要だった ―― \(\theta_2<\theta_1\) 。すると、「\(n\)大きい方が\(\theta\)小さい」つまり\(\theta\)小さい方が\(n\)大きいから、\(n_2>n_1\) 。よって全反射が起きるためには、屈折率の大きい方から小さい方へ入射することが必要である。この必要条件も入試ではよく問われるから注意しておこう。