5-12-1: 断熱自由膨張と断熱混合

練習題も込みで、急激な断熱変化の代表例を扱います。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

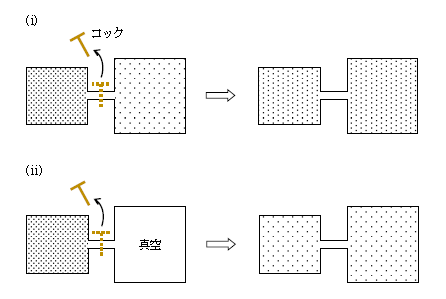
　この単元では急激な過程でおこる断熱変化の代表例2つを扱う。1つ目は「断熱混合」（図１(i)）。左右の断熱容器に気体を入れておき、次いで間のコックを外すと気体が勢いよく左から右、右から左へ流れ込み混じり合う状態変化だ。2つ目は「断熱自由膨張」（図１(ii)）。左右の断熱容器の一方にだけ気体を入れ、他方は真空にしておき、次いでコックを外すと気体が真空側に勢いよく流れ込む変化。図１右側の最終状態では圧力\(P\)や温度\(T\)など(巨視変数という)が全て一定のままに落ち着いており、これを熱平衡状態という。

　急激な変化は\(P\)-\(V\)グラフに表すことができない、と言うと驚くだろうか。というのは、変化の途中、(i)も(ii)も圧力にムラが生じている。たとえば(ii)では、左から右の容器へ気体が流入する途中、左の容器内のある領域の圧力は高いのに、右の別の領域にはまだ気体が十分届いていず圧力が低いということが起きる(圧力にムラがある)。気体全体の一様な圧力\(P\)が定義できないのだ。\(P\)が決まらなければ、（図１左側、右側の始めと終りの状態を例外として、）当然\(P\)-\(V\)グラフは書けない。(i)も全く同様。すると、5-10-1で扱った「ゆっくり」と起こる(準静的)断熱変化において成り立つ\(PV^{\gamma}= \)一定は、急激な変化では使えないと分かる。

　ところで結論を先に言うと、(i)でも(ii)でも内部エネルギーが保存している。以下1⃣2⃣に分けて説明していこう。
1⃣　断熱混合
　内部エネルギーの保存を証明するために、図１(i)左側から右側の過程で、気体AとB全体の熱力学第１法則\(Q=\Delta U+W\)を考察する。
　まず、断熱容器を想定しているから、容器の内と外で熱のやりとりはなく、\(Q=0\) 。
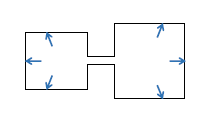
　次に気体が外部にする仕事\(W\) も０。なぜなら、混合過程中、気体は容器の内壁に圧力を加えはするが、内壁は1mm足りとも動かない（図２）。内壁の移動距離は０だ。すると気体は外部に仕事ができず\(W=0\)となる。（補足すると、気体AはBに仕事\(W_1\)をし、BはAに仕事\(W_2\)をするが、\(W_1,W_2\)は系内で起こっている話であって、外部にする仕事ではない。また、\(W_1\)と\(W_2\)は作用反作用的に打ち消し合って\(W_1+W_2=0\)である。）
　こうして\(Q=0\)及び\(W=0\)だから、熱力学第１法則より内部エネルギー変化\(\Delta U=Q-W=0\) 。変化が0だから内部エネルギーは保存する。

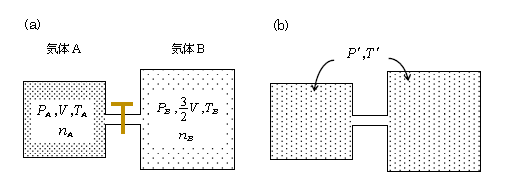
　練習題のつもりで、図３(b)における気体AとB全体の温度\(T’\)と圧力\(P’\) を求めてみよう。(b)は(a)から十分時間が経った後の熱平衡状態である。気体は単原子分子気体だとする。
　5-04-3の内部エネルギー\(\displaystyle U=\frac{3}{2}nRT\)を用いると、内部エネルギー保存則は　
　　　　　　(a)　　　　　　　　　　(b)
　\(\displaystyle \frac{3}{2}n_ART_A+\frac{3}{2}n_BRT_B \) \(=\) \(\displaystyle \frac{3}{2}(n_A+n_B)RT’ \)　　　\(\displaystyle \frac{3}{2}R \)を約分して
　　\(T’=\)\(\displaystyle \frac{n_AT_A＋n_BT_B}{n_A+n_B} \)　　[ 緑の下線は練習題に対する答という意味 ]

　次に5-04-3の\(\displaystyle U=\frac{3}{2}PV\)を用いると、図３の内部エネルギー保存則は　
　　　　　(a)　　　　　　　　　 (b)
　\(\displaystyle \frac{3}{2}P_AV +\frac{3}{2}P_B \frac{3}{2}V \) \(=\) \(\displaystyle \frac{3}{2} P’ \left( V+\frac{3}{2}V \right) \)　　　\(\displaystyle \frac{3}{2}V \)を約分して
　　\(P’=\)\(\displaystyle \frac{2}{5}P_A+\frac{3}{5}P_B \)
　というわけで、\(U=\frac{3}{2}nRT\)はもちろんのこと、\(U\)を\(P,V\)で表現した\(U=\frac{3}{2}PV\)も便利。

2⃣　断熱自由膨張
　内部エネルギー保存の証明は1⃣と同様。図４(a)から(b)（(b)は(a)から十分時間が経った熱平衡状態）で熱力学第１法則を考察する。
　断熱容器の内と外で熱のやりとりはなく、\(Q=0\) 。
　次に気体が外部にする仕事\(W\) も０。なぜなら、膨張中、気体は容器の内壁に圧力を加えはするが、内壁の移動距離は０で気体は外部に仕事ができず\(W=0\)。
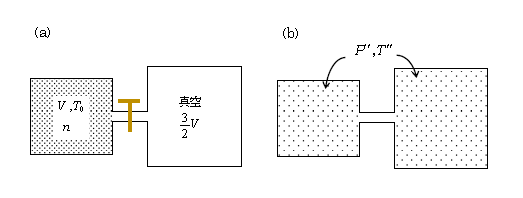
　こうして\(Q=0\)、\(W=0\)だから、熱力学第1法則より内部エネルギー変化\(\Delta U=Q-W=0\) 、すなわち内部エネルギーは保存する。再び練習題のつもりで、図４(b)における気体の温度\(T’’\)と圧力\(P’’\)を求めてみよう。気体は単原子分子気体だとする。
　\(\displaystyle U=\frac{3}{2}nRT\)を用いて内部エネルギー保存則は　
　　(a)　　　　(b)
　\(\displaystyle \frac{3}{2}nRT_0 \) \(=\) \(\displaystyle \frac{3}{2}nRT’’ \)　　　∴　\(T’’ =\) \(T_0\)
　つまり、断熱自由膨張では温度不変という結論になった。これは、「ゆっくり」と起こる(準静的)断熱膨張では温度が下がり、断熱膨張では温度が上がる（5-11-1）のと大違いである。

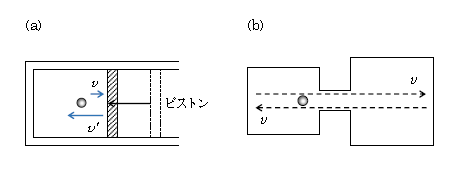
　この理由はミクロな観点で捉えると分かりやすい。5-04-3で気体分子の平均運動エネルギー \(\displaystyle \overline{\frac{m}{2} v^2}\)\(\displaystyle =\frac{3}{2} kT \) （\(k\): ボルツマン定数）の式を導いた。これによれば、右辺の温度\(T\)の上がり下がりを見るには、左辺の平均運動エネルギー\(\displaystyle \overline{\frac{m}{2} v^2}\)の増減を調べればよい。「ゆっくり」とした断熱圧縮では（図５(a)）、ピストンの移動によって分子の速さが衝突直前よりも直後の方が増す（ピストンをテニスのラケットに見立て、分子をボールにたとえれば、ラケット衝突後のボールは速くなる、といったイメージ）。ゆえに温度が上がる。
　一方、断熱自由膨張であるが（図５(b)）、気体分子運動論では5-04-1の通り、分子どうしの衝突は無視して、ピストンとの衝突を弾性衝突(はね返り係数\(e=1\))と仮定している。すると、簡単化して言えば、分子は左右の壁の間を速さを変えず往復するだけだから、温度が不変というわけである。
　図４(b)の\(P’’\)は状態方程式より　\(\displaystyle P’’=\frac{nRT’’}{V+\frac{3}{2}V}=\)\(\displaystyle \frac{2}{5}\frac{nRT_0}{V} \)