5-11-1: 等温と断熱の比較
等温変化と断熱変化の違いをしっかり押さえましょう!
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
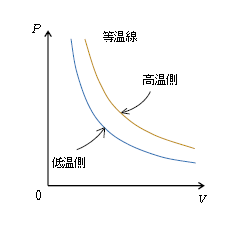
・ 等温線は\(P\)-\(V\)双曲線。高温側の等温線の方が低温側よりも原点から遠い。
・ 断熱膨張は温度が下がる。圧力も下がる。
断熱圧縮は温度が上がる。圧力も上がる。
・ 断熱線は高温側から低温側の等温線へまたがっていく右下がりの曲線。
断熱線の方が等温線よりも傾きが急。
・ 断熱変化では\(PV^{\gamma}= \)一定や\(TV^{\gamma-1} =\)一定
が成り立つ(比熱比\(\displaystyle \gamma=\frac{C_P}{C_V} \))
以下ではモル数\(n\)一定とする。5-06-1で、高校では多くの場合「準静的」過程(ピストンがほぼつり合いを保ちながらきわめてゆっくり動く過程)を扱うと述べた通り、この単元は準静的な断熱変化と等温変化をテーマとする。
まずは\(P\)-\(V\)グラフの説明から。等温変化(温度\(T\)一定)は、状態方程式\(PV=nRT\)の右辺が一定だから、圧力\(P\)と\(V\)の積\(PV=\)一定(ボイルの法則、図1)。縦軸\(P\)と横軸\(V\)の積が一定ということは、数学で言えば、\(xy=\)一定すなわち\(\displaystyle y=\frac{定数}{x} \)に相当し、グラフは双曲線となる。このとき定数の大きい方が原点から遠い双曲線になる(例えば\(\displaystyle y=\frac{1}{x} \)よりも\(\displaystyle y=\frac{5}{x} \)の方が原点から遠い)。いま、たとえば\(T=350\)Kのまま一定の等温(曲)線と、\(T=280\)Kのまま一定の等温線があるならば、\(T=350\)Kの方が高温側である。等温変化では\(\displaystyle P=\frac{nRT}{V}=\frac{定数}{V} \)だから、定数\(nRT\)の大きい高温側の等温線の方が低温側よりも原点から遠い(図1)。
次に断熱変化(熱量\(Q=0\))では、熱力学第1法則\(Q=\Delta U+W \)より\(0=\Delta U+W \) 。足して0になる2つの量は互いに逆符号(一方が正ならば他方が負)になるから、\(\Delta U\)と\(W\)は逆符号である。逆符号には2つのパターンがあって、1つ目は\(W>0\)なら\(\Delta U<0\)のパターン 。5-06-1の通り\(W>0\)のとき気体は膨張する。また5-08-1の通り\(\Delta U=nC_V\Delta T\)(\(C_V\)は定積モル比熱)だから、\(\Delta U<0\)のとき\(\Delta T<0\)、すなわち温度は下がる。よって断熱膨張は温度が下がる。
2つ目は\(W<0\)なら\(\Delta U>0\)のパターン。\(W<0\)のとき気体は圧縮(収縮)、\(\Delta U=nC_V\Delta T>0\)のとき温度は上昇。よって断熱圧縮は温度が上がる。
断熱膨張の1例は、空気の塊が地表から上昇する場合。上空は周囲の気圧が低いので空気は膨脹し、この過程が近似的に断熱と見なせて温度が下がる。(すると空気中の水蒸気が飽和して雲が発生する。)
断熱圧縮の1例は、タイヤに空気を入れる場合。空気入れの筒の中の空気は圧縮され、この過程が近似的に断熱と見なせて温度が上がる。(筒は非常に熱くなる。)
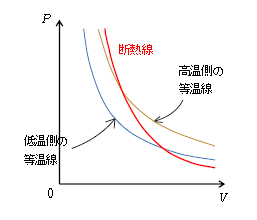
こうして、断熱(曲)線は図2のようになる。グラフの右側に行って\(V\)が増えると、断熱膨張は温度が下がるので、高温側から低温側の等温線へまたがっていく右下がりの曲線になる。
日常用語的な感覚からすると、断熱で\(Q=0\)なのになぜ温度が変化するのか?と疑問が湧くかもしれない。それはすでに上述した通り ―― \(Q=0\)だが、仕事\(W\)をすることによって内部エネルギーが変化し(\(\Delta U\)\(=nC_V\Delta T\))、温度が変化する。
一方、等温は日常用語的な感覚からすると\(Q=0\)のように思えるかもしれないが、それは誤り。正しくは、等温(\(\Delta T=0\))では\(\Delta U=nC_V\Delta T=0 \)だが、仕事\(W\)をすることによって\(Q=\Delta U+W=W \ne 0\)となる。
ところで定圧・定積モル比熱をそれぞれ\(C_P\)、\(C_V\)とすると、5-10-1の通り断熱変化では
比熱比\(\displaystyle \gamma=\frac{C_P}{C_V} \) として (1)
\(PV^{\gamma}= \)一定 (ポアソンの法則) (2)
が成り立つ。5-09-1の\(C_P=C_V+R\)(マイヤーの関係式)を(1)に代入すると、\(\displaystyle \gamma=\frac{C_V+R}{C_V}>1 \)(分子の方が分母より大きい)。すると(2)は
\(\displaystyle P=\frac{定数}{V^{\gamma}} \) (ただし\(\gamma\)>1)
となり、\(V\)が増えるほど右辺の分母が大きくなり、右辺すなわち左辺が小さくなり、\(P\)が減ると分かる(図2)。
断熱膨張は(温度だけでなく)圧力も下がる。断熱圧縮は(温度だけでなく)圧力も上がる。
なお、図2を見ると断熱線の方が等温線よりも傾きが急であることが分かる。入試の題材にしばしば取り上げられる内容だから、図2を目に焼き付けておこう。
(1)、(2)について2点補足する。
1⃣ 5-09-1の通り、単原子分子気体では\(\displaystyle C_V=\frac{3}{2} R \)、\(\displaystyle C_P=\frac{5}{2} R \)だから、(1)より単原子分子気体の\(\displaystyle \gamma=\frac{C_P}{C_V}=\frac{\frac{5}{2} R}{\frac{3}{2} R} =\frac{5}{3} \) 。この計算はスラスラできるようにしておこう。
2⃣ 状態方程式\(PV=nRT\)から得られる\(\displaystyle P=\frac{nRT}{V} \)を(2)に代入し、(2)の右辺から書くと、
一定\(\displaystyle =\frac{nRT}{V}V^{\gamma}=nR\cdot TV^{\gamma-1} \) ∴ \(TV^{\gamma-1} =\)一定 (3)
(2)をポアソンの法則の\(P\)-\(V\)表現と呼ぶことにすれば、(3)は\(T\)-\(V\)表現。(2)も(3)も出題率が高いから、頭に入れておくのがよい。
一方\(P\)-\(T\)表現をつくるには、\(PV=nRT\)から得られる\(\displaystyle V=\frac{nRT}{P} \)を(2)に代入して\(V\)を消去する。(2)の右辺から書くと、
一定\(\displaystyle =P\left(\frac{nRT}{P} \right)^{\gamma}=(nR)^{\gamma}\cdot P^{1-\gamma}T^{\gamma} \) ∴ \(\displaystyle P^{1-\gamma}T^{\gamma} =\)一定
この\(P\)-\(T\)表現は覚える必要はないが、「これを導け」といった主旨の問が出されることはあるから、\(P\)-\(T\)表現の導出計算を練習しておく必要はある。


