5-02-2: 熱量の計算 <例題>
さっそく熱量計算の例題を2題解いてみましょう!
例題1
自転車に乗っていたYさんがこぐのを止めて後輪のブレーキをかけたところ、自転車の速さが10.0m/sから5.0m/sになった。このとき、リム(車輪の外縁部)の温度が摩擦により上昇した。運動エネルギーの減少分がすべてリムの温度上昇に使われたとすると、リムの温度は何度上昇するか。最も適当な数値を、次の①~⑥のうちから1つ選べ。ただし、Yさんと自転車を合わせた質量は80\(\text{kg}\)、リムの質量は1.0\(\text{kg}\)で比熱は0.84J/\(\text{g} \cdot \)Kである。
① 0.7 ② 1.2 ③ 3.6 ④ 4.8 ⑤ 7.2 ⑥ 15
解答・解説
5-02-1の通り、熱量の計算は単位を意識しながら行おう。
リムの上昇温度を\(\Delta T \)[K]とすると、\(\Delta T \)上げるために必要な熱量は
\(0.84 \text{J}/\text{g} \cdot \text{K}×1000\text{g} × \Delta T \) [\(\text{K}\)] \(=840 \Delta T \) [\(\text{J}\)]
これが運動エネルギーの減少分 \(\displaystyle \frac{m}{2} v_0^2 – \frac{m}{2} v^2 = \frac{m}{2} (v_0^2-v^2) \)
\(\displaystyle =\frac{80\text{kg}}{2} ×(10.0^2-5.0^2) \)m\(^2 \)/s\(^2 \)\(=3000 \, \text{kg} \cdot \)m\(^2 \)/s\(^2 \)\(=3000 \, \text{J} \) に等しい。( [\(\text{kg} \cdot \)m\(^2 \)/s\(^2 \)\(= \text{J} \) ]となることは、1-16-1でやった。)
∴ \(840 \Delta T =3000 \) ∴ \(\Delta T ≒3.6 \text{K} \) 答 ③
例題2
問1 図のような熱量計(かき混ぜ棒と容器および温度計からなる)に適当な量の水を入れ、じゅうぶん時間が経過した後の温度は\(t\)であった。金属A(比熱\(c_A\) 、質量 \(m\) )をあたためて、\(t\)よりじゅうぶん高い温度\(t_0\)にした後、熱量計に入れ、かき混ぜ棒で内部の水をゆっくりかき混ぜたところ温度は\(t_1\)となった。金属Aの失った熱量はいくらか。正しいものを、次の①~④のうちから1つ選べ。
① \(c_A(t_1-t) \) ② \(c_A(t_0-t_1) \) ③ \(mc_A(t_1-t) \)
④ \(mc_A(t_0-t_1) \)
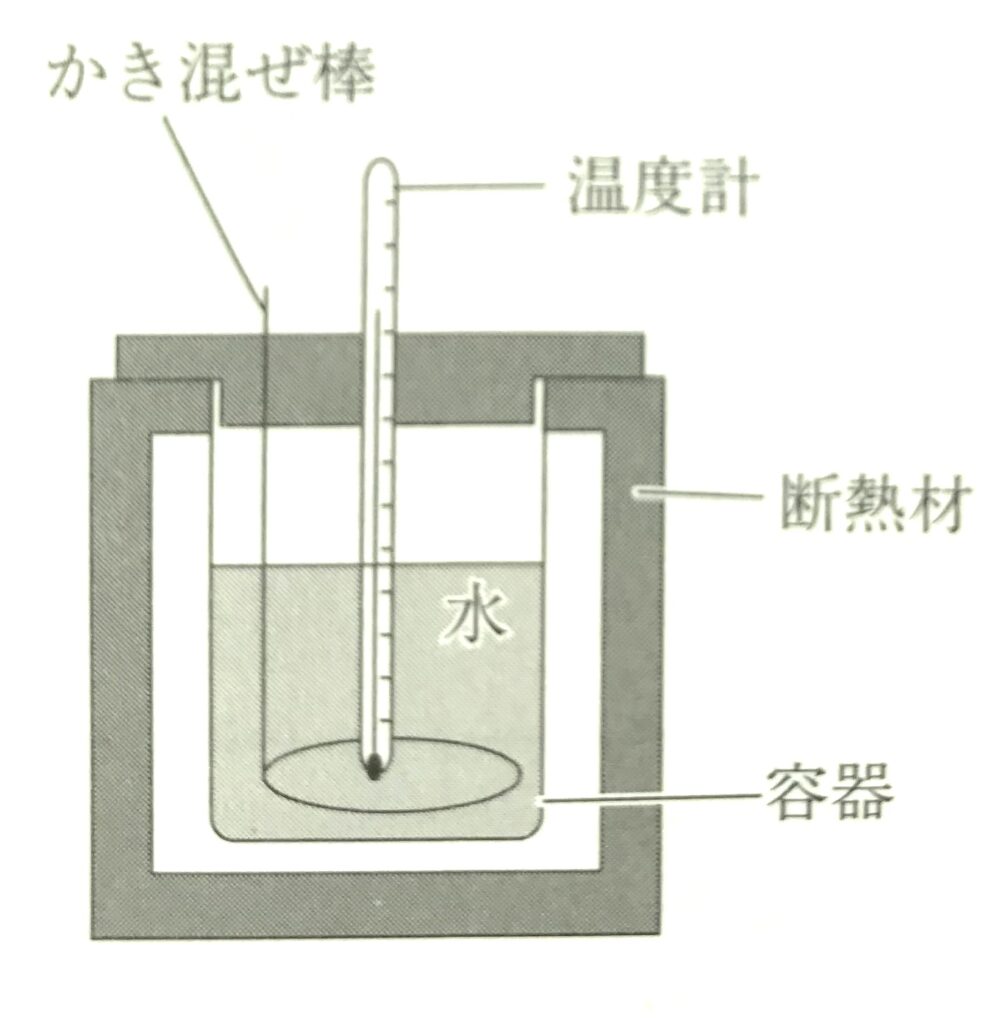
問2 次に、問1と同じ条件下で、金属Aと同じ質量の金属Bについて同じ実験を行ったところ、かき混ぜた後の温度は\(t_2\)となった。熱量計とその内部の水を合わせたもの全体の熱容量が金属Aに対する測定時と同じであることを使うと、金属Bの比熱はいくらか。正しいものを、次の①~④のうちから1つ選べ。
① \(\displaystyle c_A \frac{(t_0-t_1)(t_2-t)}{(t_0-t_2)(t_1-t)} \) ② \(\displaystyle c_A \frac{(t_0-t_2)(t_1-t)}{(t_0-t_1)(t_2-t)} \)
③ \(\displaystyle c_A \frac{(t_0-t_2)(t_0-t_1)}{(t_1-t)(t_2-t)} \) ④ \(\displaystyle c_A \frac{(t_0-t_1)(t_2-t)}{(t_0-t)(t_2-t_1)} \)
解答・解説
熱平衡に達する問題は、
1.高温物体に関する量と低温物体に関する量を図1のように整理して、
2.高温物体の失った熱量 = 低温物体の得た熱量(5-02-1) (☆) と立てればよい。
問1 図1で高温物体(金属A)の温度は\(t_0-t_1\)下がったから、
高温物体の失った熱量\(Q_A=c_A[\text{J}/\text{g} \cdot \text{K}]×m[\text{g}]×(t_0-t_1)[\text{K}] \)
\(=c_A m(t_0-t_1)[\text{J}] \) 答 ④
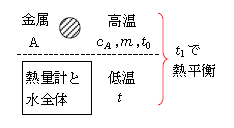
問2 低温物体(熱量計と水全体)の熱容量を\(C\)とする。まず問1で、低温物体の温度は\(t_1-t\)上がったから(図1)、
低温物体の得た熱量\(Q_X=C[\text{J}/\text{K}]×(t_1-t)[\text{K}] =C(t_1-t) [\text{J}] \)
(☆)より \(Q_A=Q_X \) ∴ \(c_A m(t_0-t_1)=C(t_1-t) \) (1)
一方、問2で(図2)
高温物体の失った熱量\(Q_B=c_B[\text{J}/\text{g} \cdot \text{K}]×m[\text{g}]×(t_0-t_2)[\text{K}] \)
\(=c_B m(t_0-t_2) [\text{J}] \)
低温物体の得た熱量\(Q’_X=C[\text{J}/\text{K}]×(t_2-t)[\text{K}] =C(t_2-t) [\text{J}] \)
(☆)より \(Q_B=Q’_X \) ∴ \(c_B m(t_0-t_2)=C(t_2-t) \) (2)
解答の選択肢を見ると、(1)、(2)から \(m,\, C\) を消去したいと分かる。
そこで(2)÷(1)とやって \(\displaystyle \frac{c_B(t_0-t_2)}{c_A(t_0-t_1)} =\frac{t_2-t}{t_1-t}\)
∴ \(\displaystyle c_B=c_A\frac{(t_0-t_1)(t_2-t)}{(t_0-t_2)(t_1-t)} \) 答 ①