3-18-1: 電流公式I=envS
電流公式はその導出の考え方をしっかり押さえた上で、覚えてしまいましょう!
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
文字\(e\),\(n\),\(v\),\(S\) については本文を参照のこと
・ 電流 \(I=envS\)
まずはミクロ、マクロという語の説明から。原子分子以下のレベルの量を微視的あるいはミクロな(microscopic)量という。分子1個の半径(10\(^{-10}\)m程度)がその例。
我々が感知できる程度に大きかったり、アボガドロ定数程度(10\(^{23}\))の大集団のレベルの量を巨視的あるいはマクロな(macroscopic)量という。例えば机はマクロな物体。
この単元では電流\(I\)を、導線中の自由電子のふるまいからミクロに説明する公式を導出する。その際の考え方は時々入試のテーマになるので、しっかり導出を追っていきたい。
3-01-1の通り、電流 \(I\)= 注目(している)断面を1sあたり通過する電気量 [C/s=A] (1)
ゆえに、図1及び図2(この後すぐに説明する)を利用して注目断面(網掛けしてある面P)を1sあたり通過する電気量を求めれば、それが\(I\)である。\(I\)は時間変化せず一定として扱うが、この単元の終りに\(I\)が変化する場合について一言述べることとする。
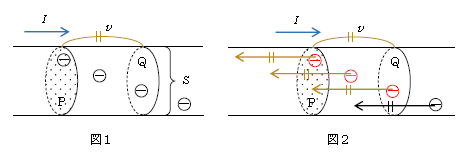
図1は円柱状の導線の拡大図で、断面積は\(S\)。ただし、正確に円柱である必要はなく、分かりやすさを考慮して円柱と呼んだまで。その中の自由電子⊝(以下、単に電子と呼ぶ)が上から順に4つ書かれている。それぞれの電子がどう配置しているかについては、次の段落で述べる。電子は負電荷なので電流\(I\)と逆向きに流れ(3-01-1)、その平均移動速度を\(v\)とする。電子の電気量の絶対値は\(e\)(電気素量という)。Qは注目断面Pより\(v\)だけ右側の断面である。図1の時刻\(t=0\)とする。
図2は図1をスタートとして「1秒間で起きること」を示した図。一番上の⊝は、\(t=0\)にPよりごくわずか右に位置している電子で、1秒後には\(v\)移動するからPを通過する。その下の⊝は、\(t=0\)にPとQのどこか中間辺りにあり、1秒後に\(v\)移動してやはりPを通過する。さらにその下の⊝は、\(t=0\)にQよりごくわずか左に位置し、\(v\)移動してぎりぎりPを通過。ところが、一番下の⊝は\(t=0\)にQよりも右にあり、\(v\)移動してもPを通過できない。
これで分かる通り、注目断面Pを1sあたり通過するのは、PとQを両底面に持つ円筒内の電子(赤色を施した電子)である。 (☆)
ここで、単位体積当りの電子数\(n\)[\(1/\text{m}^3\)]なる量を導入する(\(n\)を電子数密度という)。PとQを底面に持つ円筒の体積は\(vS\)だから
円筒内の電子数\(N=n×vS\) [\(1/\text{m}^3×\text{m}^3/\text{s}\)] (2)
(☆)より、この\(N\)が断面Pを1sあたり通過する電子数である。
こうして(1)より、
\(I=\)断面Pを1sあたり通過する電気量
\(=\)(電子1個の電気量\(e\))×(断面Pを1sあたり通過する電子数\(N\)) [(2)を代入]
\(=\)\(envS\)
これが、この単元のタイトルの電流公式である。初めに述べた通り、導出の考え方 ―― 特に図2で「1秒間で起きること」を考えて、PとQにはさまれた円筒に着目した ―― も大事であるが、この公式そのものもよく使うので、覚えてしまおう。例えば、英語のenvyという単語の複数形enviesとの語呂合わせで\(I=envS\)と丸暗記するのも一法だ。
最後に、電流 \(I\)が時々刻々変化するような場合は、図2を「微小時間\(\Delta t\)で起きること」に捉え直して、PとQの両底面間の距離を\(v\Delta t\)とする。というのも微小時間\(\Delta t\)の間では、\(I\)は事実上変化せず一定と見なせるからだ。すると断面Pを\(\Delta t\)間に通過する電子数\(\Delta N=n×v\Delta t×S\)となり、
\(I=\)Pを1sあたり通過する電気量
\(=\)(電子1個の電気量\(e\))×(Pを\(\Delta t\)間に通過する電子数\(\Delta N\))÷\(\Delta t\)
[ 1sあたりに直すために\(\Delta t\)で割った ]
\(=env\Delta t\cdot S÷\Delta t=envS \)
よって、結論は同じである。


