2-02-1: y-xグラフとy-tグラフ ＜動画あり＞

２つのグラフの違いをしっかり理解しましょう！　→　＜例題＞は2-02-2へ　　　　　　　　　　　　　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　波のグラフには、\(y\)-\(x\)グラフと\(y\)-\(t\)グラフの２種類がある。
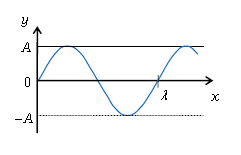
1⃣　\(y\)-\(x\)グラフ（図１）
　ひもを伝わる波を例に取ると、\(x\)座標は、ひもが真っ直ぐに張った状態での媒質粒子の位置を表す。\(y\)座標は、ひもが波立っている状態で各粒子が\(y\)方向にどれだけ変位しているか（粒子の高さ）を表す。ゆえに\(y\)-\(x\)グラフでひもの形が表わされる。
　\(y\)-\(x\)グラフは波形グラフだ。なお、\(A\)を振幅という。

2⃣　\(y\)-\(t\)グラフ
　ある１つの粒子の単振動の様子を表す\(y\)-\(t\)グラフは振動グラフだ。
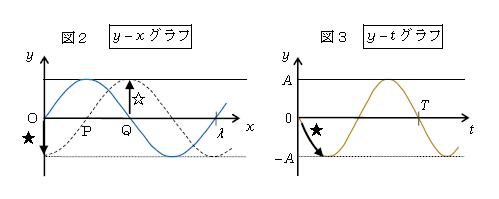
　例えば図２（\(y\)- \(x\) グラフ）で実線のサインカーブが\(t=0\)での波形、点線が\(t=\frac{T}{4}\)での波形だとする。粒子Oは\(t=0\)から\(t=\frac{T}{4}\)にかけて★のように下向きに動く（2-01-1でやった通り、粒子は\(x\)方向には動かず\(y\)方向に動く）から、横軸\(t\)の\(y\)- \(t \) グラフ（振動グラフ）で★を対応させると図３のようになる。つまり、粒子O の\(y\)-\(t\)グラフを書くときには、図２の他のP、Q、･･･は一切見ずに、Oだけを見つめ続けてその動きを追う。ということは、\(y\)-\(t\)グラフは空間的にはただ１点のことだけを表している、空間的な広がりのことは表していないグラフだ。
　　\(y\)-\(x\)グラフはある瞬間の波形をとらえる「写真」のグラフ
　　\(y\)-\(t\)グラフはある１点の振動を見つめ続ける「ビデオ」のグラフ
と理解しておくとよい。なお、
　　横軸が[m]単位の\(y\)-\(x\)グラフのサインカーブ１個分の横幅は波長\(\lambda \)[m]（図２）
　　横軸が[s]単位の\(y\)-\(t\)グラフのサインカーブ１個分の横幅は周期\(T\)[s]（図３）　　
を表す。

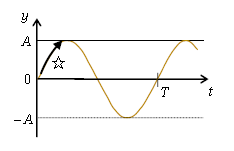
　さて、粒子Qは図２で☆のように上向きに動くから、その\(y\)-\(t\)グラフは図４のようになり、図３とは違ってくる。

　そもそも、
　\(y\)-\(t\)グラフは横軸が\(t\)で、\(t\)が変数だが、逆に\(x\)は１つに固定している（例えば\(x=0\)に固定したものが図３）。
　\(y\)-\(x\)グラフは横軸が\(x\)で、\(x\)が変数だが、逆に\(t\)は１つに固定している（例えば\(t=\frac{T}{4}\)に固定したものが図２の点線）。
　入試で波のグラフの問題が出題されたなら、まず横軸に注意しよう。その上で、
　　　\(y\)-\(x\)グラフなら\(t\)をいつに固定しているのか
　　　\(y\)-\(t\)グラフなら\(x\)をどこに固定しているのか
を押さえることが大切だ。 　
　最後に動画を見てみよう。